NumPy - 二项分布

什么是二项分布?

二项分布是一种离散概率分布，它描述在固定次数的独立试验中，每次试验的成功概率相同。

它由两个参数定义:试验次数 (n) 和每次试验的成功概率 (p)。二项分布的概率质量函数 (PMF) 给出在 n 次试验中恰好获得 k 次成功的概率。 PMF 的公式为 −

P(X = k) = C(n, k) * pk * (1 - p)(n - k)

其中 C(n, k) 是二项式系数，计算公式为 −

C(n, k) = n! / (k! * (n - k)!)

NumPy 中的二项分布

NumPy 提供了 numpy.random.binomial() 函数来根据二项分布生成样本。此函数允许您指定试验次数、成功概率以及生成样本的大小。

示例

在此示例中，我们从二项分布中生成 10 个随机样本，该分布包含 10 次试验，成功概率为 0.5 -

import numpy as np

# 从二项分布中生成 10 个随机样本，该分布包含 10 次试验，成功概率为 0.5
samples = np.random.binomial(n=10, p=0.5, size=10)
print("来自二项分布的随机样本:", sample)

以下是获得的输出 -

来自二项分布的随机样本:[5 7 5 7 1 3 5 8 7 5]

二项分布可视化

二项分布可视化有助于更好地理解其性质。我们可以使用 Matplotlib 等库来创建直方图，以显示生成样本的分布。

示例

在下面的示例中，我们首先从二项分布中生成 1000 个随机样本，其中进行了 10 次试验，成功概率为 0.5。然后，我们通过创建直方图来可视化该分布 -

import numpy as np
import matplotlib.pyplot as plt

# 从二项分布中生成 1000 个随机样本，该分布包含 10 次试验，成功概率为 0.5
samples = np.random.binomial(n=10, p=0.5, size=1000)

# 创建直方图来可视化分布
plt.hist(samples, bins=np.arange(12) - 0.5, edgecolor='black', density=True)
plt.title('Binomial Distribution')
plt.xlabel('Number of successes')
plt.ylabel('Frequency')
plt.xticks(range(11))
plt.show()

直方图显示了二项式试验中成功次数的频率。条形表示每种可能结果的概率，构成了二项分布的特征形状 -

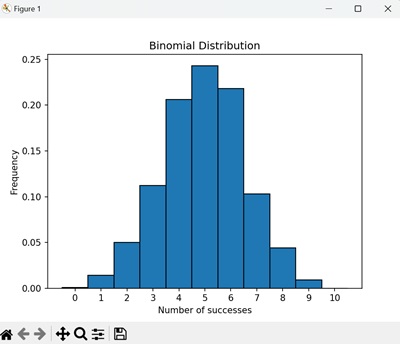
二项式分布的应用

二项式分布广泛应用于统计学、医学、质量控制和社会科学等各个领域。以下是一些实际应用 -

• 质量控制: 用于模拟一批产品中的缺陷品数量。
• 医学: 用于模拟从一组患者中治愈的患者数量。
• 调查分析: 用于模拟对调查问题做出积极回应的人数。

生成累积二项分布

有时，我们对二项分布的累积分布函数 (CDF) 感兴趣，它给出了在 n 次试验中获得最多 k 次成功的概率。

NumPy 没有内置二项分布的 CDF 函数，但我们可以使用循环和 scipy.stats.binom.cdf() 函数来计算它。 SciPy 库。

示例

在本例中，我们使用 NumPy 库生成累积二项分布 -

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

# 定义试验次数和成功概率
n = 10
p = 0.5

# 生成累积分布函数 (CDF) 值
x = np.arange(0, n+1)
cdf = binom.cdf(x, n, p)

# 绘制 CDF 值
plt.plot(x, cdf, marker='o', linestyle='-', color='b')
plt.title('累积二项分布')
plt.xlabel('成功次数')
plt.ylabel('累积概率)
plt.grid(True)
plt.show()

该图显示了二项式试验中每次成功次数的累积概率。 CDF 是一个阶跃函数，随着成功次数的增加，其值递增至 1 -

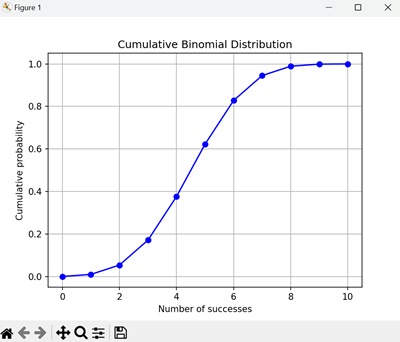
二项分布的性质

二项分布有几个关键性质，它们是 -

• 离散性:二项分布是离散的，这意味着它只接受整数值。
• 均值:二项分布的均值由 n * p 给出。
• 方差:二项分布的方差由 n * p * (1 - p) 给出。
• 对称性:当 p = 0.5 时，二项分布为对称。

二项分布的假设检验

二项分布常用于假设检验，尤其是在比例检验中。

二项分布是一种常见的检验方法，用于确定样本中成功的比例是否与指定比例存在显著差异。以下是使用 scipy.stats.binom_test() 函数的示例。

示例

在此示例中，我们执行二项分布检验来确定成功的比例(10 次中有 8 次)是否与 0.5 存在显著差异。 p值表示假设零假设成立，获得至少与观察结果同样极端的结果的概率 -

from scipy.stats import binom_test

# 成功次数
successes = 8

# 试验次数
trials = 10

# 假设的成功概率
p = 0.5

# 执行二项式检验
p_value = binom_test(successes, trials, p)
print("二项式检验的P值:", p_value)

得到的输出如下所示 -

/home/cg/root/673c4ae169586/main.py:13: DeprecationWarning: 'binom_test' 已弃用，建议使用 'binomtest'从 1.7.0 版本开始，并将在 Scipy 1.12.0 中移除。
p_value = binom_test(successes, trials, p)
二项式检验的 P 值:0.109375

种子设定以确保可重复性

为确保可重复性，您可以在生成二项分布之前设置特定的种子。这样可以确保每次运行代码时都会生成相同的随机数序列。

示例

通过设置种子，可以确保每次执行代码时随机生成的结果都相同，如下例所示 -

import numpy as np

# 设置种子以确保可重复性
np.random.seed(42)

# 从二项分布中生成 10 个随机样本，其中试验次数为 10 次，成功概率为 0.5
samples = np.random.binomial(n=10, p=0.5, size=10)
print("种子为 42 的随机样本:", sample)

生成的结果如下 -

种子为 42 的随机样本:[4 8 6 5 3 3 3 7 5 6]