NumPy - 时间序列分析

NumPy 中的时间序列分析

时间序列分析是一种用于分析按时间顺序排列的数据点的技术，例如股票价格、销售数据或温度读数。NumPy 及其数组操作允许您处理、操作和分析时间序列数据。

在本教程中，我们将探索如何使用 NumPy 进行时间序列分析，涵盖创建时间序列数组、执行统计操作以及可视化随时间变化的趋势等重要技术。

使用 NumPy 创建时间序列数据

在 NumPy 中创建时间序列通常涉及生成一个与一系列时间点对应的 datetime 对象数组。您可以使用 NumPy 的 datetime64 数据类型创建基于时间的数组。

有了时间序列后，您就可以将相关数据(例如股票价格或温度)与时间点一起存储。

示例

在以下示例中，我们将创建一个表示每日时间戳的简单时间序列数组，以及一个表示股票价格的关联数据数组 -

import numpy as np

# 为每日数据创建时间序列数组
dates = np.array(['2024-01-01', '2024-01-02', '2024-01-03', '2024-01-04', '2024-01-05'], dtype='datetime64[D]')

# 创建一个与日期对应的股票价格数组
stock_prices = np.array([150.25, 152.75, 153.50, 155.00, 154.25])

print("日期:", dates)
print("股价:", stock_prices)

输出将显示相应的时间序列数据 -

日期:['2024-01-01' '2024-01-02' '2024-01-03' '2024-01-04' '2024-01-05']
股价:[150.25 152.75 153.5 155. 154.25]

时间序列数据的统计分析

NumPy 提供了几个可用于时间序列分析的统计函数。例如，您可以计算一段时间内的平均值、标准差和累计和，以观察数据的趋势和波动。

示例

在以下示例中，我们将计算时间序列中的平均股价和股价的累计和 -

import numpy as np

# 股价时间序列
stock_prices = np.array([150.25, 152.75, 153.50, 155.00, 154.25])

# 计算平均股价
mean_price = np.mean(stock_prices)

# 计算股价的累计和
cumulative_sum = np.cumsum(stock_prices)

print("平均股价:", mean_price)
print("累计股票价格总和:",cumulative_sum)

输出结果如下 −

平均股价:153.15
股票价格累计总和:[150.25 303.   456.5  611.5  765.75]

计算随时间变化的差异和变化

在时间序列分析中，计算连续数据点之间的差异通常有助于理解随时间的变化。

NumPy 的 diff() 函数允许您计算数组中每对相邻值之间的差异，这对于识别趋势、波动性或增长率非常有用。

示例

在此示例中，我们将使用 NumPy 的diff() 函数 −

import numpy as np

# 股票价格的时间序列
stock_prices = np.array([150.25, 152.75, 153.50, 155.00, 154.25])

# 计算股票价格的每日变化
price_changes = np.diff(stock_prices)

print("价格变化:", price_changes)

输出将显示股票价格的每日变化 -

价格变化:[ 2.5   0.75  1.5  -0.75]

可视化时间序列数据

可视化时间序列数据有助于识别随时间变化的趋势、模式和异常。虽然 NumPy 没有内置绘图函数，但您可以轻松使用外部库(例如 Matplotlib)来可视化时间序列数据以及 NumPy 数组。

示例

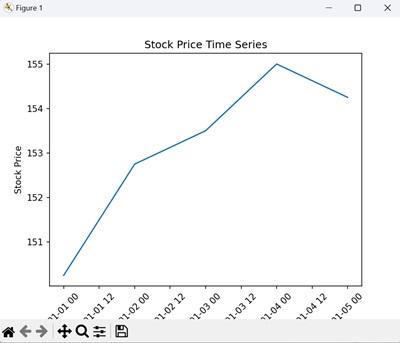
在以下示例中，我们将使用 Matplotlib 绘制股票价格的时间序列 -

import numpy as np
import matplotlib.pyplot as plt

# 日期和股票价格的时间序列
dates = np.array(['2024-01-01', '2024-01-02', '2024-01-03', '2024-01-04', '2024-01-05'], dtype='datetime64[D]')
stock_prices = np.array([150.25, 152.75, 153.50, 155.00, 154.25])

# 绘制股价随时间变化的曲线
plt.plot(dates, stock_prices)
plt.xlabel('日期')
plt.ylabel('股价')
plt.title('股价时间序列')
plt.xticks(rotation=45)
plt.show()

这将生成一个简单的折线图，显示股价随时间变化的趋势 -

重采样时间序列数据

重采样是时间序列分析中的一项重要技术，它涉及改变数据的频率。根据分析的性质，您可能需要将数据从每日重采样为每月，或从每小时重采样为每日。

虽然 NumPy 不直接提供重采样函数，但您可以使用 NumPy 的切片和聚合方法来实现这一点。

示例

在此示例中，我们将通过取每周的平均值将每日股价重采样为每周平均值 -

import numpy as np

# 10 天的每日股价
daily_prices = np.array([150.25, 152.75, 153.50, 155.00, 154.25, 156.00, 158.00, 160.25, 162.50, 163.75])

# 重新采样为每周平均值(为简单起见，假设每周 7 天)
weekly_avg = np.mean(daily_prices[:7].reshape(-1, 7), axis=1)

print("每周平均股价:", weekly_avg)

输出将显示每周平均价格 −

每周平均股价:[154.25]