NumPy - 卡方分布
什么是卡方分布?
卡方分布是一种连续概率分布,在统计学中用于检验关于总体方差或两个变量独立性的假设。
它是一种特殊的分布,由独立标准正态随机变量的平方和推导而来。从数学上讲,如果 Z1、Z2、...、Zk 是独立的标准正态变量,则 −
X = Z12 + Z22 + ... + Zk2
它由自由度 (df) 定义,自由度取决于数据集中独立变量的数量。该分布呈偏态,且随着自由度的增加而变得更加对称。
因此,得到的变量 X 服从具有 k 个自由度的卡方分布。自由度(表示为 k)在确定分布形状方面起着重要作用。自由度越高,分布越对称。
NumPy 中的卡方样本
NumPy 提供了 numpy.random.chisquare() 函数,可以从卡方分布中生成随机样本。此函数需要两个主要参数 -
- df: 自由度。
- size(可选): 要生成的样本数量。
示例:生成卡方样本
以下示例从自由度为 5 的卡方分布中生成 10 个随机样本 -
import numpy as np
# 生成卡方样本
degrees_of_freedom = 5
samples = np.random.chisquare(degrees_of_freedom, size=10)
print("生成的卡方样本:", sample)
以下是获得的输出 -
生成的卡方样本:[3.94124915 3.61732939 8.09217857 1.63322954 2.26579558 3.74957222 10.88281092 1.98262239 3.816437 10.83575014]
卡方分布的性质
卡方分布具有几个重要的性质,使其在统计分析中非常有用,它们是:
- 不对称性:分布向右偏斜,尤其是在自由度较低的情况下。自由度越大,偏度越小。
- 均值:卡方分布的均值等于其自由度 (df)。
- 方差:方差是自由度的两倍,即 2 * df。
示例
以下示例将验证给定自由度的均值和方差 -
import numpy as np
# 验证均值和方差
df = 5
samples = np.random.chisquare(df, size=1000)
mean = np.mean(samples)
variance = np.var(samples)
print("样本均值:",mean)
print("样本方差:", variance)
这将产生以下结果 −
样本平均值:5.04405316596172 样本方差:10.565774002162097
卡方分布的应用
卡方分布主要用于假设检验和方差估计。常见应用包括:-
- 拟合优度检验:评估一组观测数据与理论分布的匹配程度。
- 独立性检验:使用列联表分析两个分类变量的独立性。
- 方差分析:评估总体的变异性或比较两个总体的方差。
示例:拟合优度检验
假设我们已经观察到掷骰子的频率,并想使用卡方分布检验骰子是否公平 -
import numpy as np
# 观测频率和预期频率
observed = np.array([16, 18, 16, 14, 18, 18])
expected = np.array([15, 15, 15, 15, 15, 15])
# 卡方统计量
chi_square_stat = np.sum((observed - expected)**2 / expected)
print("卡方统计量:", chi_square_stat)
此统计量可与卡方分布表中的临界值进行比较,以确定骰子的公平性 −
卡方统计量: 2.0
卡方分布可视化
可视化有助于理解卡方分布的形状和特征卡方分布。我们可以使用 Matplotlib 绘制其概率密度函数 (PDF)。
示例:绘制卡方 PDF
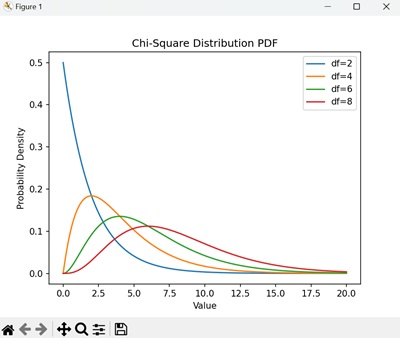
在以下示例中,我们创建了一个线图,显示不同自由度的卡方分布的 PDF -
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
# 绘制不同自由度的 PDF
x = np.linspace(0, 20, 500)
dfs = [2, 4, 6, 8]
for df in dfs:
plt.plot(x, chi2.pdf(x, df), label=f"df={df}")
plt.title("卡方分布PDF")
plt.xlabel("值")
plt.ylabel("概率密度")
plt.legend()
plt.show()
曲线展示了随着自由度的增加,分布的偏度如何减小 -
模拟真实场景
卡方分布常用于质量控制和风险分析等实际场景。让我们模拟一个制造过程中质量控制的真实示例。
示例:制造业的质量控制
假设一家工厂测量产品尺寸的变异性。卡方分布可以检验变异性是否在可接受的范围内。该统计数据可用于确定观察到的方差是否超过可接受的阈值 -
import numpy as np
# 观测方差和可接受阈值
observed_variance = 4.5
sample_size = 20
population_variance = 4.0
# 卡方统计量
chi_square_stat = (sample_size - 1) * observed_variance / population_variance
print("卡方统计量:", chi_square_stat)
我们得到如下所示的输出 −
卡方统计量: 21.375

