NumPy - 正态分布

什么是正态分布?

正态分布，也称为高斯分布，是一种围绕均值对称的连续概率分布，这意味着接近均值的数据比远离均值的数据出现的频率更高。

正态分布的形状由其均值 () 和标准差 () 描述。均值决定了分布的中心，而标准差控制了数据的散布。

NumPy 中的正态分布

NumPy 提供了 numpy.random.normal() 函数来生成正态分布的样本。此函数允许您指定生成样本的平均值、标准差和大小。

示例

在此示例中，我们从平均值为 0、标准差为 1 的正态分布中生成 10 个随机样本 -

import numpy as np

# 从平均值为 0、标准差为 1 的正态分布中生成 10 个随机样本
samples = np.random.normal(0, 1, 10)
print("来自正态分布的随机样本:", sample)

以下是获得的输出 -

来自正态分布的随机样本:[ 1.45958315 -1.47376803  0.86885907  0.28076705 -2.16173553 -0.43457503
0.47706858  0.65894456  0.56166159 -0.71025105]

可视化正态分布

可视化正态分布有助于更好地理解其特性。我们可以使用 Matplotlib 等库来创建直方图，以显示生成样本的分布。

示例

在以下示例中，我们将从均值为 0、标准差为 1 的正态分布中生成 1000 个随机样本，然后创建一个直方图来可视化该分布 -

import numpy as np
import matplotlib.pyplot as plt

# 从均值为 0、标准差为 1 的正态分布中生成 1000 个随机样本
samples = np.random.normal(0, 1, 1000)

# 创建直方图来可视化分布
plt.hist(samples, bins=30, edgecolor='black', density=True)

# 绘制概率密度函数 (PDF)
x = np.linspace(-4, 4, 1000)
pdf = 1/(np.sqrt(2 * np.pi)) * np.exp(-x**2 / 2)
plt.plot(x, pdf, 'r', linewidth=2)
plt.title('正态分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()

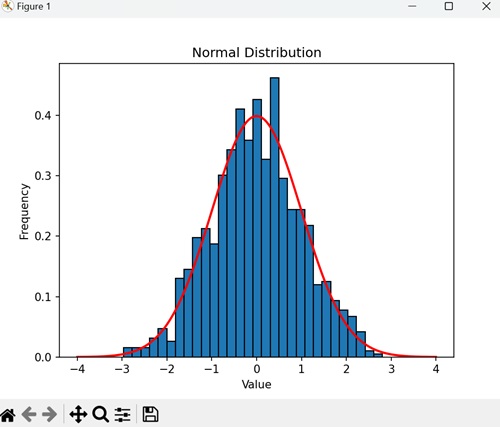
直方图显示样本服从钟形曲线，这是正态分布的特征。红线表示正态分布的理论概率密度函数 (PDF) −

正态分布的应用

正态分布广泛应用于统计学、金融学、工程学以及自然科学和社会科学等各个领域。以下是一些实际应用:

• 统计分析:许多统计检验和方法假设数据服从正态分布。
• 质量控制:在制造业中，正态分布用于监控流程。
• 金融:资产收益通常使用正态分布建模。

生成多元正态分布

NumPy 还允许使用 numpy.random.multivariate_normal() 函数从多元正态分布生成样本。此函数从具有指定均值向量和协方差矩阵的多元正态分布生成样本。

示例

在此示例中，我们从具有指定均值向量和协方差矩阵的多元正态分布中生成 1000 个随机样本 -

import numpy as np

# 定义均值向量和协方差矩阵
mean = [0, 0]
cov = [[1, 0.5], [0.5, 1]]

# 从多元正态分布中生成 1000 个随机样本
samples = np.random.multivariate_normal(mean, cov, 1000)

print("从多元正态分布中生成的随机样本:", sample[:5])

输出结果如下 −

从多元正态分布中生成的随机样本:
[[-0.13543463 1.3100422 ]
[-1.46447528 -0.42485422]
[ 0.31941286 -0.33503219]
[ 0.86726151 1.43161159]
[ 0.12539345 -1.72856329]]

正态分布的性质

正态分布有几个关键性质，它们是:-

• 对称性:正态分布围绕均值对称。
• 均值、中位数和众数:在正态分布中，均值、中位数和众数都相等。
• 经验法则:大约 68% 的数据落在均值的一个标准差范围内，95% 的数据落在均值的两个标准差范围内，99.7% 的数据落在均值的三个标准差范围内。

标准正态分布

标准正态分布是正态分布的一个特例平均值为 0，标准差为 1。它通常用作参考分布。您可以使用 numpy.random.standard_normal() 函数从标准正态分布中生成样本。

示例

在此示例中，我们从标准正态分布中生成 10 个随机样本 -

import numpy as np

# 从标准正态分布中生成 10 个随机样本
samples = np.random.standard_normal(10)
print("从标准正态分布中随机抽取的样本:", sample)

生成的结果如下 -

从标准正态分布中随机抽取的样本:[ 0.41271088 -0.06102183 -0.48159376  0.63379932 -0.41831826 -0.67104197
0.2019988   0.52954154 -0.39241029 -0.19626287]

种子设定以确保可重复性

为确保可重复性，您可以在生成正态分布之前设置特定的种子。这样可以确保每次运行代码时都会生成相同的随机数序列。

示例

通过设置种子，可以确保每次执行代码时随机生成的结果都相同，如下例所示 -

import numpy as np

# 设置种子以确保可重复性
np.random.seed(42)

# 从均值为 0、标准差为 1 的正态分布中生成 10 个随机样本
samples = np.random.normal(0, 1, 10)
print("种子为 42 的随机样本:", sample)

我们得到如下所示的输出 -

种子为 42 的随机样本:[ 0.49671415 -0.1382643   0.64768854  1.52302986 -0.23415337 -0.23413696
  1.57921282  0.76743473 -0.46947439  0.54256004]