NumPy - 使用 Seaborn 可视化分布
使用 Seaborn 可视化分布
处理数据时,可视化分布是理解数据特征的重要一步。
Seaborn 构建于 Matplotlib 之上,是一个强大的 Python 可视化库,可以简化创建信息丰富且美观的统计图表的过程。
在本教程中,我们将探索如何使用 Seaborn 可视化不同类型的分布,包括正态分布、均匀分布和其他概率分布。我们还将演示如何使用自定义选项和样式来增强可视化效果。
什么是 Seaborn?
Seaborn 是一个 Python 可视化库,它提供了一个高级接口,用于创建美观且信息丰富的统计图形。它与 Pandas 数据结构完美集成,并提供多种函数来可视化数据的分布、关系和趋势。
其主要优势之一是能够以最少的代码轻松可视化分布、相关性和数据关系。
Seaborn 基于 Matplotlib 构建,并提供更精简的函数来创建复杂的图表。它还能自动处理美观性,例如配色方案和标签,使您的可视化效果更具吸引力,更易于解读。
设置 Seaborn
在开始使用 Seaborn 可视化分布之前,我们需要安装必要的库并设置环境。如果尚未安装 Seaborn,您可以使用 pip 安装,如下所示 -
# 使用 pip 安装 Seaborn !pip install seaborn
除了 Seaborn,我们还将使用 NumPy 生成分布数据。以下是导入这两个库的典型设置 -
import seaborn as sns import numpy as np import matplotlib.pyplot as plt
导入库后,我们就可以开始生成和可视化不同类型的分布了。
可视化正态分布
正态分布是统计学中最常用的分布之一,也称为高斯分布。它是对称的钟形分布,常用于对测试分数、身高和测量误差等进行建模。
我们可以使用 NumPy 的 numpy.random.normal() 函数从正态分布中生成随机数据,然后使用 Seaborn 的 seaborn.histplot() 函数来可视化该分布。
示例
在下面的示例中,sns.histplot() 函数自动创建数据的直方图,并通过将 kde 参数设置为 True,在直方图上添加平滑的核密度估计 (KDE) 曲线,以可视化概率密度函数 (PDF) −
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 从正态分布生成随机数据
data = np.random.normal(loc=0, scale=1, size=1000)
# 使用 Seaborn 可视化分布
# kde=True 添加核密度估计曲线
sns.histplot(data, kde=True)
plt.title('正态分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()
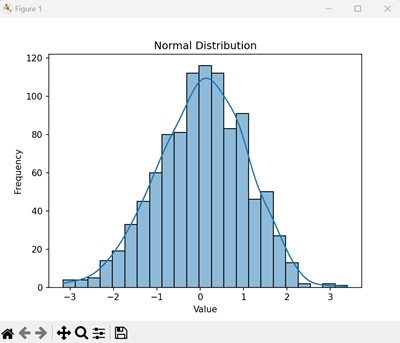
生成的图将显示钟形曲线,这是正态分布的特征 -
可视化均匀分布
均匀分布是一种所有结果都相等的分布可能性很大。在连续均匀分布中,数据点均匀分布在给定范围内。
我们可以使用 NumPy 的 numpy.random.uniform() 函数生成均匀分布的数据,并使用 Seaborn 进行可视化。
示例
此处,numpy.random.uniform() 函数生成介于指定低值和高值(在本例中为 0 和 10)之间的随机数。直方图呈现平坦分布,表明所有值在指定范围内出现的可能性均等 -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 生成均匀分布的随机数据
data_uniform = np.random.uniform(low=0, high=10, size=1000)
# 使用 Seaborn 可视化分布
sns.histplot(data_uniform, kde=True)
plt.title('均匀分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()
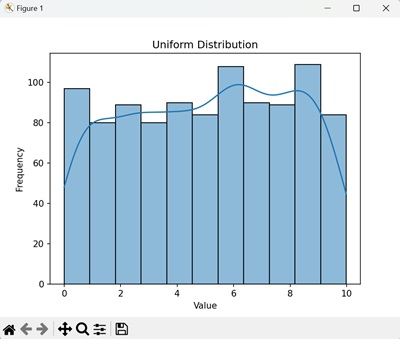
生成的输出将显示均匀分布,其中每个值的频率在整个范围内大致相同 -
指数分布可视化
指数分布通常用于对泊松过程中事件间隔时间进行建模。它具有偏向性,小值出现的频率较高,而大值出现较长的尾部。
NumPy 提供了 numpy.random.exponential() 函数,用于根据指数分布生成随机数据。
示例
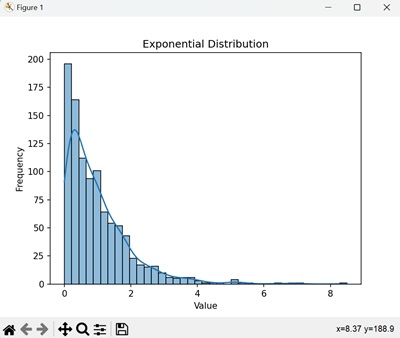
在下面的示例中,我们将创建一个绘图,该绘图将显示峰值接近零且尾部向右延伸的分布。这是指数分布的一个特征,即某个值出现的概率会随着该值的增加而呈指数下降 -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 根据指数分布生成随机数据
data_exponential = np.random.exponential(scale=1, size=1000)
# 使用 Seaborn 可视化分布
sns.histplot(data_exponential, kde=True)
plt.title('Exponential Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
我们得到如下所示的输出 -
可视化帕累托分布
正如我们之前讨论过的,帕累托分布遵循幂律,在经济学中常用于模拟财富分配。您可以使用 NumPy 的 numpy.random.pareto() 函数生成帕累托分布的数据。
示例
使用 Seaborn 可视化帕累托分布 -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 从帕累托分布生成随机数据
# 加 1 移动最小值
data_pareto = np.random.pareto(a=2, size=1000) + 1
# 使用 Seaborn 可视化分布
sns.histplot(data_pareto, kde=True)
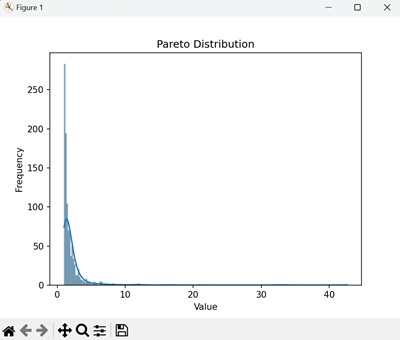
plt.title('Pareto分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()
帕累托分布将显示高度偏斜的直方图,其长尾向右延伸,反映出少数大值在数据集中占主导地位 -
自定义 Seaborn 绘图
Seaborn 允许您轻松自定义绘图的外观。例如,您可以调整直方图中的箱数、更改绘图的颜色,甚至修改绘图的样式。以下是自定义外观的几种方法 -
- 更改箱数: 您可以通过指定 bins 参数来控制直方图中箱数。
- 更改颜色: 使用 color 参数为绘图设置自定义颜色。
- 修改样式: Seaborn 提供了几种内置样式(例如 'darkgrid'、'whitegrid' 等),可以使用 sns.set_style() 应用于绘图。
示例
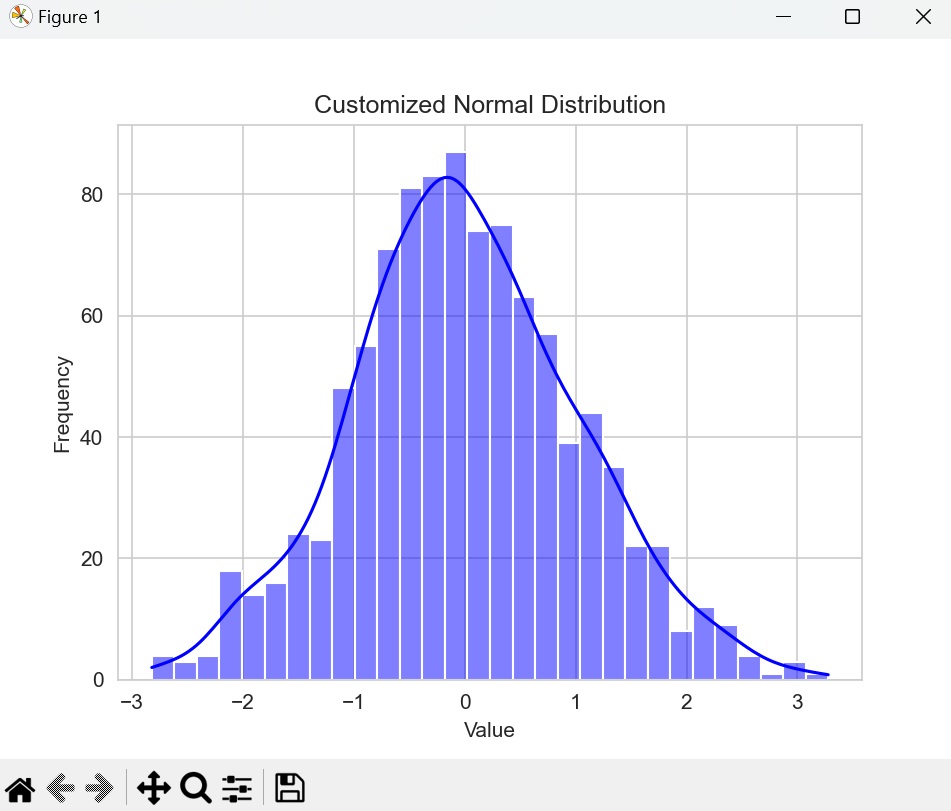
在下面的示例中,我们将创建一个包含 30 个箱、蓝色和白色网格背景的绘图 -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 根据正态分布生成随机数据
data = np.random.normal(loc=0, scale=1, size=1000)
# 自定义绘图样式
sns.set_style('whitegrid')
# 使用更多 bins 和自定义颜色进行绘图
sns.histplot(data, bins=30, color='blue', kde=True)
plt.title('自定义正态分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()
生成的结果如下 -