---

网络理论 - 双端口网络

一般来说，如果用等效模型表示任何电网络，并给出输入和输出变量之间的关系，则很容易分析它。为此，我们可以使用双端口网络表示。顾名思义，双端口网络包含两个端口。其中一个端口用作输入端口，另一个端口用作输出端口。第一和第二个端口分别称为端口 1 和端口 2。

单端口网络是一个双端电网络，其中电流通过一个端子进入，通过另一个端子流出。电阻器、电感器和电容器是单端口网络的例子，因为每个都有两个端子。下图显示了单端口网络表示。

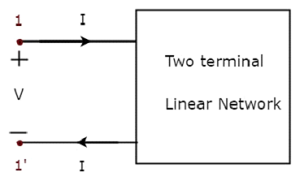
这里，一对端子 1 和 1' 表示一个端口。在这种情况下，我们只有一个端口，因为它是一个单端口网络。

类似地，双端口网络是一对双端电网络，其中电流通过一个端子进入，并通过每个端口的另一个端子离开。下图显示了双端口网络表示。

这里，一对端子 1 和 1' 代表一个端口，称为 端口 1，另一对端子 2 和 2' 代表另一个端口，称为 端口 2。

如图所示，双端口网络中有 四个变量 V₁、V₂、I₁ 和 I₂。其中，我们可以选择两个变量作为独立变量，另两个变量作为因变量。因此，我们将得到六对可能的方程。这些方程用独立变量来表示因变量。独立变量的系数称为参数。因此，每对方程将给出一组四个参数。

双端口网络参数

双端口网络的参数称为双端口网络参数或简称为双端口参数。以下是双端口网络参数的类型。

• Z 参数
• Y 参数
• T 参数
• T' 参数
• h 参数
• g 参数

现在，让我们逐一讨论这两个端口网络参数。

Z 参数

我们将变量 V₁ 和 V₂ 视为相关变量，将 I₁ 和 I₂ 视为独立变量，从而得到以下两个方程组。独立变量 I₁ 和 I₂ 的系数称为 Z 参数。

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

Z 参数 为

$$Z_{11} = \frac{V_1}{I_1}, \: 当 \: I_2 = 0$$

$$Z_{12} = \frac{V_1}{I_2}, \: 当 \: I_1 = 0$$

$$Z_{21} = \frac{V_2}{I_1}, \: 当 \: I_2 = 0$$

$$Z_{22} = \frac{V_2}{I_2}, \: 当 \: I_1 = 0$$时

Z 参数被称为阻抗参数，因为它们只是电压和电流的比率。Z 参数的单位是欧姆 (Ω)。

我们可以通过开通端口 2 来计算两个 Z 参数，Z₁₁ 和 Z₂₁。同样，我们可以通过开通端口 1 来计算另外两个 Z 参数，Z₁₂ 和 Z₂₂。因此，Z 参数也称为开路阻抗参数。

Y 参数

通过考虑变量 I₁ &，我们将得到以下两个方程组I₂ 为依赖关系，V₁ & V₂ 为独立关系。独立变量 V₁ 和 V₂ 的系数称为 Y 参数。

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

Y 参数 为

$$Y_{11} = \frac{I_1}{V_1}, \: 当 \: V_2 = 0$$

$$Y_{12} = \frac{I_1}{V_2}, \: 当 \: V_1 = 0$$

$$Y_{21} = \frac{I_2}{V_1}, \: 当 \: V_2 = 0$$

$$Y_{22} = \frac{I_2}{V_2}, \: 当 \: V_1 = 0$$

Y 参数被称为导纳参数，因为它们只是电流和电压的比率。Y 参数的单位是姆欧。

我们可以通过短路端口 2 来计算两个 Y 参数，Y₁₁ 和 Y₂₁。同样，我们可以通过短路端口 1 来计算另外两个 Y 参数，Y₁₂ 和 Y₂₂。因此，Y 参数也称为短路导纳参数。

T 参数

我们将变量 V₁ 和 I₁ 视为相关变量，将 V₂ 和 I₂ 视为独立变量，从而得到以下两个方程组。 V₂ 和 -I₂ 的系数称为 T 参数。

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

T 参数 为

$$A = \frac{V_1}{V_2}, \: 当 \: I_2 = 0$$

$$B = -\frac{V_1}{I_2}, \: 当 \: V_2 = 0$$

$$C = \frac{I_1}{V_2}, \: 当 \: I_2 = 0$$

$$D = -\frac{I_1}{I_2}, \: 当 \: V_2 = 0$$

T 参数称为传输参数或 ABCD 参数。参数 A 和 D 没有单位，因为它们是无量纲的。参数 B 和 C 的单位分别是欧姆和姆欧。

我们可以通过开路端口 2 来计算两个参数 A 和 C。同样，我们可以通过短路端口 2 来计算另外两个参数 B 和 D。

T 参数

我们将变量 V₂ 和 I₂ 视为相关变量，将 V₁ 和 I₁ 视为独立变量，将得到以下两个方程组。 V₁ 和 -I₁ 的系数被称为 T' 参数。

$$V_2 = A' V_1 - B' I_1$$

$$I_2 = C' V_1 - D' I_1$$

T' 参数 为

$$A' = \frac{V_2}{V_1}, \: 当\: I_1 = 0$$

$$B' = -\frac{V_2}{I_1}, \: 当\: V_1 = 0$$

$$C' = \frac{I_2}{V_1}, \: 当\: I_1 = 0$$

$$D' = -\frac{I_2}{I_1}, \: 当 \: V_1 = 0$$ 时

T' 参数称为逆传输参数或 A'B'C'D' 参数。参数 A' 和 D' 没有任何单位，因为它们是无量纲的。参数 B' 和 C' 的单位分别是欧姆和姆欧。

我们可以通过对端口 1 进行开路来计算两个参数 A' 和 C'。同样，我们可以通过对端口 1 进行短路来计算另外两个参数 B' 和 D'。

h 参数

通过将变量 V₁ 和 I₂ 视为相关变量，将 I₁ 和 V₂ 视为独立变量，我们将得到以下两个方程组。独立变量 I₁ 和 V₂ 的系数称为 h 参数。

$$V_1 = h_{11} I_1 + h_{12} V_2$$

$$I_2 = h_{21} I_1 + h_{22} V_2$$

h 参数为

$$h_{11} = \frac{V_1}{I_1},\: 当\: V_2 = 0$$

$$h_{12} = \frac{V_1}{V_2},\: 当\: I_1 = 0$$

$$h_{21} = \frac{I_2}{I_1},\: 当\: V_2 = 0$$

$$h_{22} = \frac{I_2}{V_2},\: 当\: I_1 = 0$$

h 参数被称为混合参数。参数 h₁₂ 和 h₂₁ 没有任何单位，因为它们是无量纲的。参数 h₁₁ 和 h₂₂ 的单位分别是欧姆和姆欧。

我们可以通过短路端口 2 来计算两个参数 h₁₁ 和 h₂₁。类似地，我们可以通过开路端口 1 来计算另外两个参数 h₁₂ 和 h₂₂。

h 参数或混合参数在晶体管建模电路（网络）中很有用。

g 参数

我们将变量 I₁ 和 V₂ 视为因变量，将 V₁ 和 I₂ 视为独立变量，从而得到以下两个方程组。独立变量 V₁ 和 I₂ 的系数称为 g 参数。

$$I_1 = g_{11} V_1 + g_{12} I_2$$

$$V_2 = g_{21} V_1 + g_{22} I_2$$

g 参数为

$$g_{11} = \frac{I_1}{V_1},\: 当\: I_2 = 0$$

$$g_{12} = \frac{I_1}{I_2},\: 当\: V_1 = 0$$

$$g_{21} = \frac{V_2}{V_1},\: 当\: I_2 = 0$$

$$g_{22} = \frac{V_2}{I_2},\: 当 \: V_1 = 0$$

g 参数被称为逆混合参数。参数 g₁₂ 和 g₂₁ 没有任何单位，因为它们是无量纲的。参数 g₁₁ 和 g₂₂ 的单位分别是姆欧和欧姆。

我们可以通过开路端口 2 来计算两个参数 g₁₁ 和 g₂₁。同样，我们可以通过短路端口 1 来计算另外两个参数 g₁₂ 和 g₂₂。

---