电量分割原理

在本章中，我们来讨论以下两种电量分割原理。

• 电流分割原理
• 电压分割原理

电流分割原理

当两个或多个无源元件并联时，流过每个元件的电流量会从进入节点的电流中分割（共享）。

考虑以下电路图。

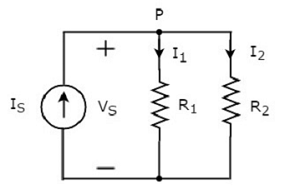
上述电路图由一个输入电流源I_S与两个电阻器R₁并联组成和R₂。每个元件两端的电压为V_S。流过电阻器 R₁ 和 R₂ 的电流分别为 I₁ 和 I₂。

节点 P 处的 KCL 方程 将是

$$I_S = I_1 + I_2$$

• 将 $I_1 = \frac{V_S}{R_1}$ 和 $I_2 = \frac{V_S}{R_2}$ 代入上述方程中。

$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} = V_S \lgroup \frac {R_2 + R_1 }{R_1 R_2} group$$

$$\Rightarrow V_S = I_S \lgroup \frac{R_1R_2}{R_1 + R_2} group$$

• 将 V_S 的值代入 $I_1 = \frac{V_S}{R_1}$ 中。

$$I_1 = \frac{I_S}{R_1}\lgroup \frac{R_1 R_2}{R_1 + R_2} group$$

$$\Rightarrow I_1 = I_S\lgroup \frac{R_2}{R_1 + R_2} group$$

• 将V_S 中的 $I_2 = \frac{V_S}{R_2}$。

$$I_2 = \frac{I_S}{R_2} \lgroup \frac{R_1 R_2}{R_1 + R_2} group$$

$$\Rightarrow I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} group$$

从 I₁ 和 I₂ 方程式中，我们可以概括出，流过任何无源元件的电流都可以使用以下公式找到。

$$I_N = I_S \lgroup \frac{Z_1 Vert Z_2 Vert... Vert Z_{N-1}}{Z_1 + Z_2 + ... + Z_N} group$$

这被称为电流分配原理，当两个或多个无源元件并联连接且只有一个电流进入节点时，该原理适用。

其中，

• I_N 是流过第 N 个分支的无源元件的电流。

• I_S 是进入节点的输入电流。

• Z₁、Z₂、…、Z_N 分别是第 1 个分支、第 2 个分支、…、第 N 个分支的阻抗。

分压原理

当两个或多个无源元件串联连接时，每个元件上的电压量会从整个组合上的可用电压中分配（共享）。

考虑以下电路图。

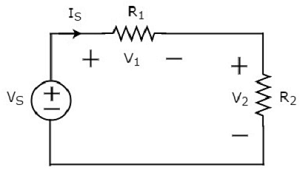
上述电路图由一个电压源 V_S 与两个电阻 R₁ 和 R₂ 串联组成。流过这些元件的电流为 I_S。电阻 R₁ 和 R₂ 两端的电压降分别为 V₁ 和 V₂。

环路周围的 KVL 方程 将是

$$V_S = V_1 + V_2$$

• 在上述方程中代入 V₁ = I_S R₁ 和 V₂ = I_S R₂

$$V_S = I_S R_1 + I_S R_2 = I_S(R_1 + R_2)$$

$$I_S = \frac{V_S}{R_1 + R_2}$$

• 将 I_S 的值代入 V₁ = I_S R₁ 中。

$$V_1 = \lgroup \frac {V_S}{R_1 + R_2} group R_1$$

$$\Rightarrow V_1 = V_S \lgroup \frac {R_1}{R_1 + R_2} group$$

• 将 I_S 的值代入 V₂ = I_S 中R₂。

$$V_2 = \lgroup \frac {V_S}{R_1 + R_2} group R_2$$

$$\Rightarrow V_2 = V_S \lgroup \frac {R_2}{R_1 + R_2} group$$

从V₁和V₂的方程式中，我们可以概括出，任何无源元件两端的电压都可以使用以下公式找到。

$$V_N = V_S \lgroup \frac {Z_N}{Z_1 + Z_2 +....+ Z_N} group$$

这被称为分压原理，当两个或多个无源元件串联连接且只有一个电压时，它适用整个组合上均有。

其中，

• V_N 是第 N 个无源元件两端的电压。

• V_S 是输入电压，存在于整个串联无源元件组合上。

• Z₁、Z₂、…、Z₃ 分别为第 1 个无源元件、第 2 个无源元件、…、第 N 个无源元件的阻抗。