网络理论 - 基尔霍夫定律
网络元素可以是主动或被动类型。任何电路或网络都包含这两种类型的网络元素之一或两者的组合。
现在,让我们讨论以下两个定律,它们通常被称为基尔霍夫定律。
- 基尔霍夫电流定律
- 基尔霍夫电压定律
基尔霍夫电流定律
基尔霍夫电流定律 (KCL) 指出,离开(或进入)节点的电流的代数和等于零。
节点是两个或多个电路元素连接到它的点。如果只有两个电路元件连接到一个节点,那么该节点被称为简单节点。如果三个或更多电路元件连接到一个节点,则称该节点为主节点。
从数学上讲,KCL 可以表示为
$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$
其中,
Im 为离开该节点的第 m 个分支电流。
M 为连接到该节点的分支数。
上述KCL的说法也可以表示为"进入节点的电流的代数和等于离开节点的电流的代数和"。让我们通过以下示例来验证此陈述。
示例
在下图的节点P处写出KCL方程。
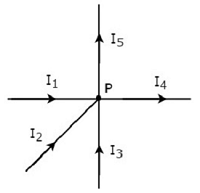
在上图中,分支电流I1、I2和I3在节点P处进入。因此,考虑这三个电流的负号。
在上图中,分支电流I4和I5从节点P处离开。因此,考虑这两个电流的正号。
节点P处的KCL方程将是
$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$
$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$
在上面的等式中,左边表示进入电流的总和,而右边表示离开电流的总和。
在本教程中,我们将考虑电流离开节点时的正号和进入节点时的负号。同样,您可以考虑电流离开节点时的负号和进入节点时的正号。在这两种情况下,结果相同。
注意 − KCL 与连接到节点的网络元素的性质无关。
基尔霍夫电压定律
基尔霍夫电压定律 (KVL) 指出,环路或网格周围的电压代数和等于零。
环路是一条终止于其起始点的同一节点的路径。相反,Mesh 是一个内部不包含任何其他环路的环路。
从数学上讲,KVL 可以表示为
$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$
其中,
Vn 是环路(网格)中第 n 个元素的电压。
N 是环路(网格)中的网络元素数量。
上述 KVL 陈述也可以表示为"电压源的代数和等于环路中存在的电压降的代数和。"让我们借助以下示例来验证此陈述。
示例
围绕以下电路的回路写出KVL 方程。
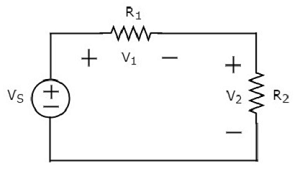
上述电路图由一个电压源 VS 与两个电阻器 R1 和 R2 串联组成。电阻 R1 和 R2 两端的电压降分别为 V1 和 V2。
在环路周围应用 KVL。
$$V_S - V_1 - V_2 = 0$$
$$\Rightarrow V_S = V_1 + V_2$$
在上面的等式中,左侧项表示单个电压源 VS。而右侧表示电压降的总和。在此示例中,我们仅考虑了一个电压源。这就是为什么左侧仅包含一个项的原因。如果我们考虑多个电压源,则左侧包含电压源的总和。
在本教程中,我们将每个元件电压的符号视为在环路中行进时存在的第二个端子的极性。类似地,您可以将每个电压的符号视为在环路中传播时出现的第一个端子的极性。在这两种情况下,结果将相同。
注意 − KVL 与环路中存在的网络元素的性质无关。


