网络理论 - 交流电路的响应
在上一章中,我们讨论了直流电路的瞬态响应和稳态响应。在本章中,我们来讨论一下交流电路的响应。我们在上一章中讨论过的瞬态响应和稳态响应的概念在这里也会很有用。
查找串联 RL 电路的响应
考虑以下串联 RL 电路图。
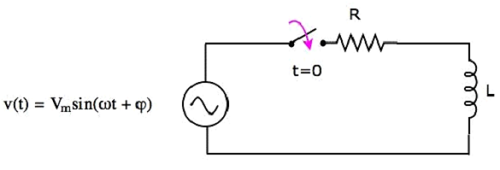
在上述电路中,开关保持打开直到t = 0,并在t = 0时关闭。因此,直到此刻,峰值电压为 Vm 伏的交流电压源尚未连接到串联 RL 电路。因此,没有初始电流流过电感器。
当开关处于闭合位置时,电路图如下图所示。
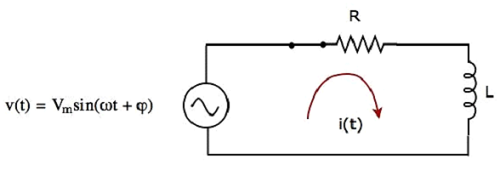
现在,电流i(t)流过整个电路,因为峰值电压为Vm伏的交流电压源连接到串联 RL 电路。
我们知道,流过上述电路的电流i(t)将有两个项,一个代表瞬态部分,另一个代表稳定状态。
从数学上讲,它可以表示为
$i(t) = i_{Tr}(t) + i_{ss}(t)$公式1
其中,
$i_{Tr}(t)$为流过电路的电流的瞬态响应。
$i_{ss}(t)$为流过电路的电流的稳态响应。
在上一章中,我们得到了流过串联RL电路的电流的瞬态响应。它的形式为 $Ke^{-\lgroup \frac{t}{ au} group}$。
将 $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{ au} group}$ 代入公式 1。
$i(t) = Ke^{-\lgroup \frac{t}{ au} group} + i_{ss}(t)$公式 2
稳态电流的计算
如果将正弦信号作为线性电路的输入,则它会产生稳态输出,这也是一个正弦信号。输入和输出正弦信号的频率相同,但幅度和相位角不同。
我们可以使用拉普拉斯变换方法计算电路在正弦电压源激励下的稳态响应。
当开关处于闭合位置时,下图显示了 s 域电路图。
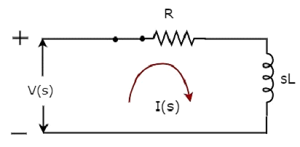
在上述电路中,所有数量和参数均以s 域表示。这些是时域数量和参数的拉普拉斯变换。
上述电路的传递函数为
$$H(s) = \frac{I(s)}{V(s)}$$
$$\Rightarrow H(s) = \frac{1}{Z(s)}$$
$$\Rightarrow H(s) = \frac{1}{R + sL}$$
Substitute $s = j \omega$ in the above equation.
$$H(j \omega) = \frac{1}{R + j \omega L}$$
Magnitude of $\mathbf{\mathit{H(j \omega)}}$ is
$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$
Phase angle of $\mathbf{\mathit{H(j \omega)}}$ is
$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} group$$
通过执行以下两个步骤 −,我们将获得稳态电流 $i_{ss}(t)$。
将输入正弦电压的峰值电压与 $H(j \omega)$ 的幅度相乘。
将输入正弦电压和 $H(j \omega)$ 的相位角相加。
稳态电流 $i_{ss}(t)$ 将是
$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$$
将 $i_{ss}(t)$ 的值代入公式 2。
$i(t) = Ke^{-\lgroup \frac{t}{ au} group} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$公式 3
我们知道电路中没有初始电流。因此,代入 t = 0 & i(t) = 0,以便找到常数 K 的值。
$$0 = Ke^{-\lgroup \frac{0}{ au} group} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$$
$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$$
$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$$
将公式 3 中的 K 值代入公式 3 中。
$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group e^{-\lgroup \frac{t}{ au} group} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$公式 4
公式 4 表示当串联 RL 电路受正弦电压源激励时,流经该电路的电流。它有两个项。第一项和第二项分别表示电流的瞬态响应和稳态响应。
我们可以忽略公式 4 的第一项,因为它的值将远小于一。因此,流过电路的最终电流将是
$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R} group group$$
它仅包含稳态项。因此,我们只能找到交流电路的稳态响应,而忽略其瞬态响应。


