网络理论 - 直流电路的响应
如果电路对输入的输出随时间变化,则称为时间响应。时间响应由以下两部分组成。
- 瞬态响应
- 稳态响应
在本章中,我们首先讨论这两种响应,然后在串联 RL 电路中观察这两种响应,当它由直流电压源激励时。
瞬态响应
将输入施加到电路后,输出需要一定的时间才能达到稳定状态。因此,输出将处于瞬态,直到进入稳定状态。因此,电路在瞬态期间的响应称为瞬态响应。
对于较大的"t"值,瞬态响应将为零。理想情况下,"t" 的这个值应该是无穷大。但是,实际上 五个时间常数 就足够了。
瞬态的存在或不存在
由于施加到电路中的源的突然变化和/或由于开关动作,响应中会发生瞬态。有两种可能的开关动作。它们是打开开关和关闭开关。
如果电路或网络仅包含电阻,则瞬态部分将不出现。因为电阻器具有调节任意电压和电流的能力。
由于电感器和电容器等储能元件的存在,瞬态部分出现在电路或网络的响应中。因为它们无法立即改变存储在这些元件中的能量。
电感器行为
假设开关动作发生在 t = 0 时。当开关动作发生时,电感器电流不会瞬间改变。这意味着,开关动作之后的电感器电流值将与开关动作之前的值相同。
从数学上讲,它可以表示为
$$i_L (0^+) = i_L (0^-)$$
电容器行为
当开关动作发生时,电容器电压不会像电感器电流那样瞬间改变。这意味着,开关动作后电容电压的值将与开关动作前电容电压的值相同。
从数学上讲,它可以表示为
$$v_c (0^+) = v_c (0^-)$$
稳态响应
对于较大的"t"值,即使瞬态响应变为零值后仍保留的时间响应部分称为稳态响应。这意味着,在稳定状态下,响应中不会有任何瞬态部分。
电感器行为
如果独立源长时间连接到具有一个或多个电感器和电阻器(可选)的电路或网络,则该电路或网络被称为处于稳定状态。因此,该电路电感器中存储的能量最大且恒定。
从数学上讲,它可以表示为
$W_L = \frac{L {i_L}^2}{2} = $ Maximum & constant
$\Rightarrow i_L = $ Maximum & constant
因此,电感器在稳定状态下充当恒流源。
电感器两端的电压为
$$V_L = L \frac{di_{L}}{dt} = 0V$$
因此,电感器在稳定状态下充当短路。
电容器行为
如果独立源长时间连接到具有一个或多个电容器和电阻器(可选)的电路或网络,则该电路或网络被称为处于稳定状态。因此,该电路电容器中存储的能量最大且恒定。
从数学上讲,它可以表示为
$W_c = \frac{C{v_c}^2}{2} = $ 最大值 & 常数
$\Rightarrow v_c = $最大值 &恒定
因此,电容器在稳定状态下充当恒定电压源。
流过电容器的电流将是
$$i_c = C\frac{dv_c}{dt} = 0A$$
因此,电容器在稳定状态下充当开路。
查找串联 RL 电路的响应
考虑以下串联 RL 电路图。
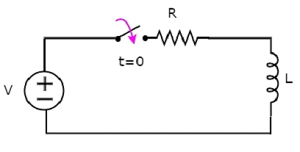
在上述电路中,开关保持打开直到 t = 0,并在 t = 0 时关闭。因此,具有 V 伏的直流电压源未连接到串联RL 电路直至此刻。因此,没有初始电流流过电感器。
当开关处于关闭位置时,电路图如下图所示。
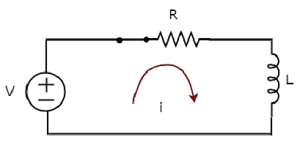
现在,电流i流过整个电路,因为具有V伏的直流电压源连接到串联 RL 电路。
现在,在环路周围应用KVL。
$$V = Ri + L \frac{di}{dt}$$
$\frac{di}{dt} + \lgroup \frac{R}{L} group i = \frac{V}{L}$公式 1
上述公式为一阶微分方程,其形式为
$\frac{dy}{dt} + Py = Q$公式 2
通过比较公式 1 和公式 2,我们将得到以下关系。
$$x = t$$
$$y = i$$
$$P = \frac{R}{L}$$
$$Q = \frac{V}{L}$$
公式 2 的 解 为
$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$公式 3
其中,k 为常数。
代入 x、y、P 和 的值;公式 3 中的 Q。
$ie^{\int {\lgroup \frac{R}{L} group}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} group}dt} group dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} group t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} group t} dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} group t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} group}t}{\frac{R}{L}} brace + k$
$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} group}t$公式 4
我们知道电路中没有初始电流。因此,在公式 4 中代入 t = 0 和 𝑖 = 0,以便找到常数 k 的值。
$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} group(0)}$$
$$0 = \frac{V}{R} + k(1)$$
$$k = - \frac{V}{R}$$
代入公式 4 中的 k 值。
$$i = \frac{V}{R} + \lgroup - \frac{V}{R} group e^{-\lgroup \frac{R}{L} group t}$$
$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} group t}$$
因此,流过电路的电流为
$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} group t} + \frac{V}{R}$公式 5
因此,当串联 RL 电路受到直流电压源激励时,其响应具有以下两个项。
第一项 $-\frac{V}{R}e^{-\lgroup \frac{R}{L} group t}$ 对应于瞬态响应。
第二项 $\frac{V}{R}$ 对应于稳态响应。这两个响应如下图所示。
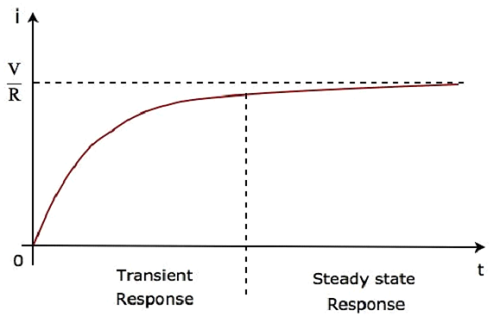
我们可以将公式 5 重写如下 −
$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} group t} group$
$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{ au} group} group$公式 6
其中, τ 是时间常数,其值等于 $\frac{L}{R}$。
公式 5 和公式 6 相同。但是,我们可以通过代入公式 6 中的几个 t 值(如 0、τ、2τ、5τ 等)轻松理解上述流过电路的电流波形。
在上述流过电路的电流波形中,瞬态响应将从零开始呈现最多五个时间常数,而稳态响应将从五个时间常数开始呈现。


