网络理论 - 诺顿定理

诺顿定理与戴维南定理类似。它指出，任何两端线性网络或电路都可以用等效网络或电路表示，该网络或电路由一个电流源与一个电阻并联组成。它被称为诺顿等效电路。线性电路可能包含独立源、从属源和电阻器。

如果电路具有多个独立源、从属源和电阻器，则可以通过用诺顿等效电路替换该元件左侧的整个网络来轻松找到元件中的响应。

元件中的响应可以是该元件两端的电压、流过该元件的电流或该元件两端耗散的功率。

下图说明了此概念。

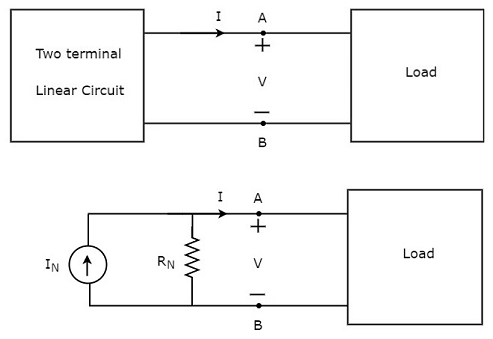
诺顿等效电路类似于实际电流源。因此，它有一个与电阻并联的电流源。

• 诺顿等效电路中存在的电流源称为诺顿等效电流或简称为诺顿电流 I_N。

• 诺顿等效电路中存在的电阻称为诺顿等效电阻或简称为诺顿电阻 R_N。

查找诺顿等效电路的方法

有三种方法可以查找诺顿等效电路。根据网络中存在的源类型，我们可以选择这三种方法之一。现在，让我们逐一讨论这三种方法。

方法 1

当仅存在独立类型源时，请按照以下步骤找到诺顿等效电路。

• 步骤 1 − 考虑电路图，打开端子，找到 Norton 等效电路。

• 步骤 2 − 通过短路上述电路的两个开路端子，找到 Norton 电流 I_N。

• 步骤 3 − 通过消除步骤 1 中考虑的电路中存在的独立源，找到电路开路端子之间的 Norton 电阻 R_N。Norton 电阻 R_N 将与 Thevenin 电阻 R_Th 相同。

• 步骤 4 −通过将诺顿电流 IN 与诺顿电阻 R_N 并联，绘制 诺顿等效电路。

现在，我们可以在位于诺顿等效电路右侧的元件中找到响应。

方法 2

当存在 独立类型和依赖类型 的源时，请按照以下步骤找到诺顿等效电路。

• 步骤 1 − 考虑电路图，打开要找到诺顿等效电路的端子。

• 步骤 2 −找到上述电路开路端子之间的开路电压 V_OC。

• 步骤 3 − 通过短路上述电路的两个开路端子找到 Norton 的电流 I_N。

• 步骤 4 − 使用以下公式找到 Norton 的电阻 R_N。

$$R_N = \frac{V_{OC}}{I_N}$$

• 步骤 5 − 通过将诺顿电流 I_N 与诺顿电阻 R_N 并联，绘制诺顿等效电路。

现在，我们可以在位于诺顿等效电路右侧的元件中找到响应。

方法 3

这是查找诺顿等效电路的另一种方法。

• 步骤 1 − 在所需的两个端子之间找到 戴维南等效电路。我们知道它由戴维南电压源 V_Th 和戴维南电阻 R_Th 组成。

• 步骤 2 −将源变换技术应用于上述戴维南等效电路。我们将得到诺顿等效电路。这里，

诺顿电流，

$$I_N = \frac{V_{Th}}{R_{Th}}$$

诺顿电阻，

$$R_N = R_{Th}$$

下图说明了这一概念。

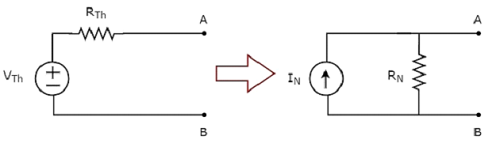
现在，我们可以通过将诺顿等效电路放在该元素的左侧来找到该元素中的响应。

注意 − 类似地，我们可以通过先找到诺顿等效电路，然后对其应用源变换技术来找到戴维南等效电路。下图说明了此概念。

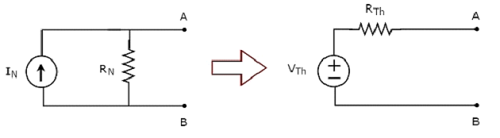
这是查找戴维南等效电路的方法 3。

示例

首先在端子 A 和 B 左侧找到 诺顿等效电路，然后找到流过 20 Ω 电阻的电流。

让我们使用方法 3来解决这个问题。

步骤 1 − 在上一章中，我们计算了端子 A 和 B 左侧的戴维南等效电路。我们现在可以使用该电路。如下图所示。

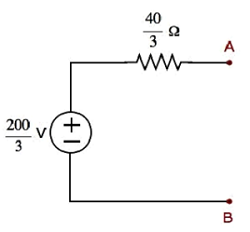
这里，戴维南电压 $V_{Th} = \frac{200}{3} V$ 和戴维南电阻 $R_{Th} = \frac{40}{3} \Omega$

步骤 2 − 将源变换技术应用于上述戴维南等效电路。将 V_Th 和 R_Th 的值代入以下 诺顿电流 公式中。

$$I_N = \frac{V_{Th}}{R_{Th}}$$

$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$

因此，诺顿电流 I_N 为 5 A。

我们知道诺顿电阻 R_N 与戴维南电阻 R_Th 相同。

$$\mathbf {R_N = \frac{40}{3} \Omega}$$

与上述戴维南等效电路相对应的诺顿等效电路如下图所示。

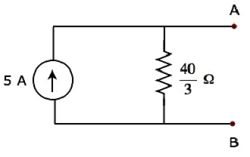
现在，将诺顿等效电路放置在端子 A & 的左侧给定电路的 B。

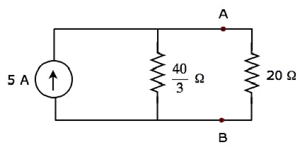
通过使用电流分配原理，流过 20 Ω 电阻的电流将是

$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} group$$

$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} group = 2A$$

因此，流过 20 Ω 电阻的电流为 2 A。