网络理论 - 无源元件
在本章中,我们将详细讨论电阻器、电感器和电容器等无源元件。让我们从电阻器开始。
电阻器
电阻器的主要功能是阻止或限制电流的流动。因此,使用电阻器是为了限制电流量和/或分配(共享)电压。
假设流过电阻器的电流为 I 安培,电阻器两端的电压为 V 伏。下图显示了电阻的符号以及电流 I 和电压 V。

根据欧姆定律,电阻两端的电压是流过电阻的电流与该电阻的电阻的乘积。 从数学上来说,它可以表示为
$V = IR$ 公式 1
$\Rightarrow I = \frac{V}{R}$公式 2
其中,R 是电阻器的电阻。
从公式 2,我们可以得出结论,流过电阻器的电流与施加在电阻器上的电压成正比,与电阻器的电阻成反比。
电路元件中的功率可以表示为
$P = VI$公式 3
将公式 1 代入公式 3。
$P = (IR)I$
$\Rightarrow P = I^2 R$公式 4
将公式 2 代入公式 3。
$P = V \lgroup \frac{V}{R} group$
$\Rightarrow P = \frac{V^2}{R}$ 公式 5
因此,我们可以使用公式 3 至公式 5 中提到的公式之一来计算电阻器中耗散的功率。
电感器
一般来说,电感器会有许多匝数。因此,当电流流过时,它们会产生磁通量。所以,电感产生的总磁通量取决于流过电感的电流I,两者呈线性关系。
从数学上讲,可以写成
$$\Psi \: \alpha \: I$$
$$\Rightarrow \Psi = LI$$
其中,
Ψ为总磁通量
L为电感的电感量
设流过电感的电流为I安培,电感两端的电压为V伏。电感器的符号以及电流I和电压V如下图所示。
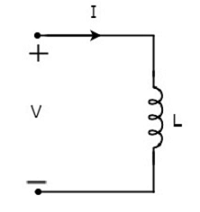
根据法拉第定律,电感器两端的电压可以写成
$$V = \frac{d\Psi}{dt}$$
将 Ψ = LI 代入上述方程。
$$V = \frac{d(LI)}{dt}$$
$$\Rightarrow V = L \frac{dI}{dt}$$
$$\Rightarrow I = \frac{1}{L} \int V dt$$
从上述方程式中,我们可以得出结论,电感两端的电压与流过电感的电流之间存在线性关系。
我们知道,电路元件中的功率可以表示为
$$P = VI$$
将 $V = L \frac{dI}{dt}$ 代入上述方程。
$$P = \lgroup L \frac{dI}{dt} group I$$
$$\Rightarrow P = LI \frac{dI}{dt}$$
通过对上述方程进行积分,我们将得到电感中存储的能量为
$$W = \frac{1}{2} LI^2$$
因此,电感以磁场的形式存储能量。
电容器
一般来说,电容器有两个导电板,由介电介质隔开。如果在电容器上施加正电压,则它会存储正电荷。同样,如果在电容器上施加负电压,则它会存储负电荷。
因此,电容器中存储的电荷量取决于施加在其上的电压V,并且它们具有线性关系。从数学上来说,它可以写成
$$Q \: \alpha \: V$$
$$\Rightarrow Q = CV$$
其中,
Q是电容器中存储的电荷。
C是电容器的电容。
设流过电容器的电流为I安培,电容器两端的电压为V伏。下图显示了电容器的符号以及电流I和电压V。
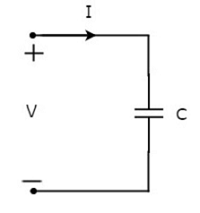
我们知道电流只不过是电荷流动的时间速率。从数学上来说,它可以表示为
$$I = \frac{dQ}{dt}$$
将$Q = CV$代入上述等式中。
$$I = \frac{d(CV)}{dt}$$
$$\Rightarrow I = C \frac{dV}{dt}$$
$$\Rightarrow V = \frac{1}{C} \int I dt$$
从上述等式中,我们可以得出结论,电容器两端的电压与流过电容器的电流之间存在线性关系。
我们知道,电路元件中的功率可以表示为
$$P = VI$$
将$I = C \frac{dV}{dt}$代入上述等式中方程。
$$P = V \lgroup C \frac{dV}{dt} group$$
$$\Rightarrow P = CV \frac{dV}{dt}$$
通过对上述方程进行积分,我们将得到电容器中存储的能量为
$$W = \frac{1}{2}CV^2$$
因此,电容器以电场的形式存储能量。


