网络理论 - 叠加定理

叠加定理基于电路响应与激励之间的线性概念。它指出，当多个独立源同时作用时，线性电路特定分支中的响应等于每个独立源每次作用所产生的响应之和。

在此方法中，我们每次仅考虑一个独立源。因此，我们必须从电路中消除剩余的独立源。我们可以通过短路电压源的两个端子来消除电压源，同样，也可以通过断开电流源的两个端子来消除电流源。

因此，如果有'n'个独立源，我们需要'n'次找到特定分支中的响应。特定分支中的响应可以是流过该分支的电流，也可以是跨该分支的电压。

叠加定理程序

按照以下步骤使用叠加定理找到特定分支中的响应。

步骤 1 − 通过考虑一个独立源并消除网络中存在的其余独立源来找到特定分支中的响应。

步骤 2 − 对网络中存在的所有独立源重复步骤 1。

步骤 3 − 当网络中存在所有独立源时，将所有响应相加以获得特定分支中的总体响应。

找到流过 20 Ω 的电流使用叠加定理计算以下电路的电阻。

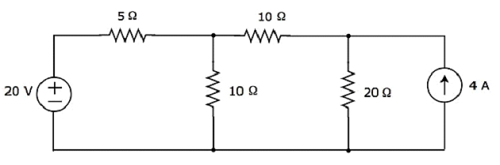
步骤 1 − 让我们通过仅考虑20 V 电压源来找到流过 20 Ω 电阻的电流。在这种情况下，我们可以通过将其开路来消除 4 A 电流源。修改后的电路图如下图所示。

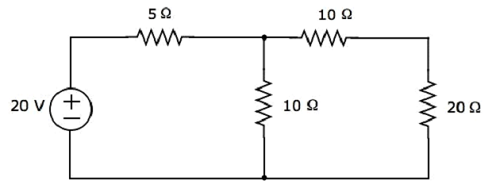
上述电路中除了地之外只有一个主节点。因此，我们可以使用节点分析方法。节点电压 V₁ 在下图中标记。这里，V₁ 是节点 1 相对于地面的电压。

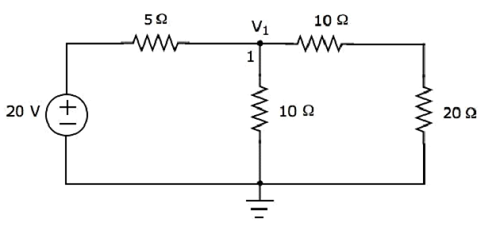
节点 1 处的节点方程是

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1}{10 + 20} = 0$$

$$\Rightarrow \frac{6V_1 - 120 + 3V_1 + V_1}{30} = 0$$

$$\Rightarrow 10V_1 = 120$$

$$\Rightarrow V_1 = 12V$$

通过进行以下简化，可以找到流过 20 Ω 电阻的电流。

$$I_1 = \frac{V_1}{10 + 20}$$

将 V₁ 的值代入上述公式中。

$$I_1 = \frac{12}{10 + 20} = \frac{12}{30} = 0.4 A$$

因此，当仅考虑 20 V 电压源时，流过 20 Ω 电阻的电流为 0.4 A。

步骤 2 − 让我们通过仅考虑 4 A 电流源来找到流过 20 Ω 电阻的电流。在这种情况下，我们可以通过短路来消除 20 V 电压源。修改后的电路图如下图所示。

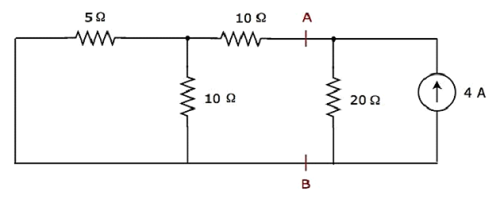
在上面的电路中，端子 A 和 B 左侧有三个电阻器。我们可以用单个等效电阻替换这些电阻器。这里，5 Ω 和 10 Ω 电阻器并联连接，整个组合与 10 Ω 电阻器串联。

端子 A 和 B 左侧的等效电阻 B 将是

$$R_{AB} = \lgroup \frac{5 imes 10}{5 + 10} group + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$

简化的电路图如下图所示。

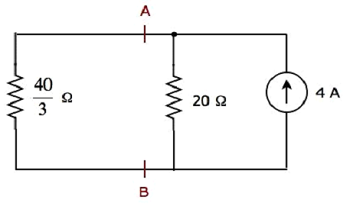
我们可以发现流过 20 Ω电阻，通过使用电流分流原理。

$$I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} group$$

将$I_S = 4A,\: R_1 = \frac{40}{3} \Omega$和$R_2 = 20 \Omega$代入上述等式中。

$$I_2 = 4 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} group = 4 \lgroup \frac{40}{100} group = 1.6 A$$

因此，流过20 Ω当仅考虑 4 A 电流源时，电阻的电流为 1.6 A。

步骤 3 − 我们将通过步骤 1 和步骤 2 中获得的两个电流相加来获得流过给定电路的 20 Ω 电阻的电流。从数学上讲，它可以写成

$$I = I_1 + I_2$$

代入上述等式中的 I₁ 和 I₂ 的值。

$$I = 0.4 + 1.6 = 2 A$$

因此，流过给定电路的 20 Ω 电阻的电流为 2 A。

注意 −我们不能直接应用叠加定理来计算传输到线性电路中任何电阻的功率量，而只能通过将每个独立源传输到该电阻的功率相加来计算。相反，我们可以利用叠加定理计算流过该电阻的总电流或跨该电阻的电压，然后利用 $I^2 R$ 或 $\frac{V^2}{R}$ 计算传输到该电阻的功率。