网络理论 - 网格分析

在网格分析中，我们将考虑流过每个网格的电流。因此，网格分析也称为网格电流方法。

分支是连接两个节点的路径，它包含一个电路元件。如果一个分支只属于一个网格，那么分支电流将等于网格电流。

如果一个分支是两个网格共有的，那么当两个网格电流方向相同（或相反）时，分支电流将等于两个网格电流的总和（或差值）。

网格分析程序

使用网格分析解决任何电气网络或电路时，请遵循以下步骤。

• 步骤 1 −识别网格并按顺时针或逆时针方向标记网格电流。

• 步骤 2 − 观察流过每个单元的网格电流量。

• 步骤 3 − 为所有网格写出网格方程。先应用 KVL，然后应用欧姆定律，即可获得网格方程。

• 步骤 4 −求解步骤 3 中获得的网格方程，以获得网格电流。

现在，我们可以使用网格电流找到流过给定网络中任何元件的电流和任何元件两端的电压。

示例

使用网格分析找到 30 Ω 电阻两端的电压。

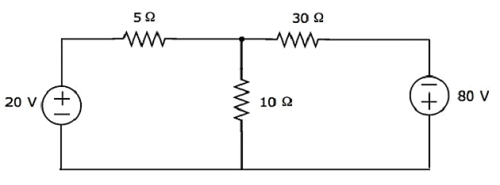
步骤 1 − 上述电路中有两个网格。网格电流 I₁ 和 I₂ 按顺时针方向考虑。这些网格电流如下图所示。

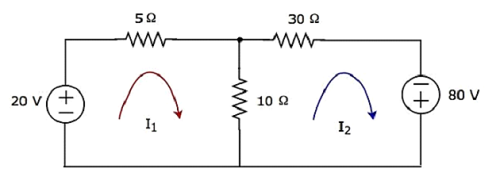
步骤 2 − 网格电流 I₁ 流过 20 V 电压源和 5 Ω 电阻。同样，网格电流 I₂ 流过 30 Ω 电阻和 -80 V 电压源。但是，两个网格电流 I₁ 和 I₂ 之差流过 10 Ω 电阻，因为它是两个网格的公共分支。

步骤 3 − 在这种情况下，我们将得到 两个网格方程，因为给定电路中有两个网格。当我们写出网格方程时，假设该特定网格的网格电流大于电路中所有其他网格电流。

第一个网格的网格方程是

$$20 - 5I_1 -10(I_1 - I_2) = 0$$

$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$

$$\Rightarrow 10I_2 = 15I_1 - 20$$

将上述方程除以 5。

$$2I_2 = 3I_1 - 4$$

将上面的等式乘以 2。

$4I_2 = 6I_1 - 8$ 等式 1

第二个网格的网格方程是

$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$

将上面的等式除以 10。

$$-(I_2 - I_1) - 3I_2 + 8 = 0$$

$$\Rightarrow -4I_2 + I_1 + 8 = 0$$

$4I_2 = I_1 + 8$ 公式 2

步骤 4 − 通过求解公式 1 和公式 2 找到网格电流 I₁ 和 I₂。

公式 1 和公式 2 的左侧项相同。因此，将公式 1 和公式 2 的右侧项相等，以找到 I₁ 的值。

$$6I_1 - 8 = I_1 + 8$$

$$\Rightarrow 5I_1 = 16$$

$$\Rightarrow I_1 = \frac{16}{5} A$$

将 I₁ 值代入公式 2。

$$4I_2 = \frac{16}{5} + 8$$

$$\Rightarrow 4I_2 = \frac{56}{5}$$

$$\Rightarrow I_2 = \frac{14}{5} A$$

因此，我们得到的网状电流I₁和I₂分别为$\mathbf{\frac{16}{5}}$ A和$\mathbf{\frac{14}{5}}$ A。

步骤 5 − 流过 30 Ω 电阻的电流就是网状电流I₂，它等于$\frac{14}{5}$ A。现在，我们可以找到 30 Ω 两端的电压电阻。

$$V_{30 \Omega} = I_2 R$$

在上述方程中代入 I₂ 和 R 的值。

$$V_{30 \Omega} = \lgroup \frac{14}{5} group 30$$

$$\Rightarrow V_{30 \Omega} = 84V$$

因此，给定电路的 30 Ω 电阻两端的电压为 84 V。

注释 1 − 从上面的例子，我们可以得出结论，如果电路有'm'个网格，我们必须求解'm'个网格方程。这就是为什么当任何电路的网格数小于主节点（参考节点除外）的数量时，我们可以选择网格分析。

注释 2 − 当任何电路的网格数等于主节点（参考节点除外）的数量时，我们可以选择节点分析或网格分析。