网络理论 - 节点分析
有两种基本方法可用于解决任何电网:节点分析和网格分析。在本章中,我们将讨论节点分析方法。
在节点分析中,我们将考虑相对于地的节点电压。因此,节点分析也称为节点电压法。
节点分析程序
在使用节点分析解决任何电网或电路时,请遵循以下步骤。
步骤 1 − 确定主要节点并选择其中一个作为参考节点。我们将该参考节点视为地。
步骤 2 −标记除参考节点外所有主要节点相对于地的节点电压。
步骤 3 − 在所有主要节点(除参考节点外)处写出节点方程。节点方程是通过先应用 KCL,然后应用欧姆定律获得的。
步骤 4 − 求解步骤 3 中获得的节点方程以获得节点电压。
现在,我们可以使用节点电压找到流过任何元件的电流以及给定网络中存在的任何元件两端的电压。
示例
找到流过 20 Ω 的电流使用节点分析计算以下电路的电阻。
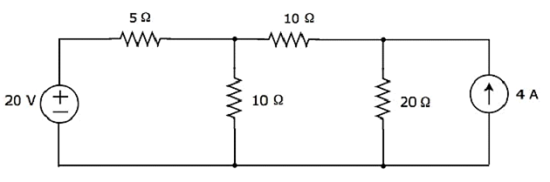
步骤 1 − 上述电路中有三个主要节点。在下图中,它们被标记为 1、2 和 3。
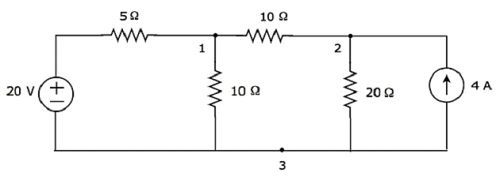
在上图中,将节点 3视为参考节点(接地)。
步骤 2 −节点电压 V1 和 V2 在下图中进行了标记。
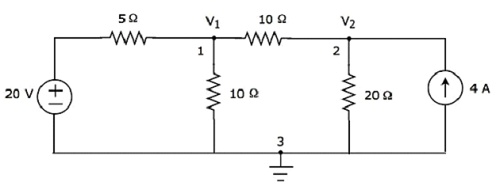
在上图中,V1 是节点 1 相对于地的电压,V2 是节点 2 相对于地的电压。
步骤 3 − 在这种情况下,我们将得到 两个节点方程,因为除了地之外,还有两个主要节点 1 和 2。当我们在节点处写出节点方程时,假设所有电流都从未提及电流方向的节点流出,并且该节点的电压大于电路中其他节点的电压。
节点 1 处的节点方程为
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$
$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$
$$\Rightarrow 4V_1 - 40 - V_2 = 0$$
$\Rightarrow V_2 = 4V_1 - 40$ 方程 1
节点 2 处的节点方程为
$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$
$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$
$\Rightarrow 3V_2 − 2V_1 = 80$ 方程 2
步骤 4 −通过求解方程 1 和方程 2 找到节点电压 V1 和 V2。
将方程 1 代入方程 2。
$$3(4 V_1 - 40) - 2 V_1 = 80$$
$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$
$$\Rightarrow 10 V_1 = 200$$
$$\Rightarrow V_1 = 20V$$
将 V1 = 20 V 代入方程 1。
$$V_2 = 4(20) - 40$$
$$\Rightarrow V_2 = 40V$$
因此,我们得到节点电压 V1 和 V2 分别为 20 V 和 40 V。
步骤 5 − 20 Ω 电阻两端的电压就是节点电压 V2,等于 40 V。现在,我们可以找到流过 20 Ω 的电流电阻。
$$I_{20 \Omega} = \frac{V_2}{R}$$
在上述公式中代入 V2 和 R 的值。
$$I_{20 \Omega} = \frac{40}{20}$$
$$\Rightarrow I_{20 \Omega} = 2A$$
因此,流过给定电路的 20 Ω 电阻的电流为 2 A。
注意 − 从上面的例子,我们可以得出结论,如果电路有'n'个主节点(参考节点除外),我们必须求解'n'个节点方程。因此,当主节点数(参考节点除外)小于任何电路的网格数时,我们可以选择节点分析。


