最大功率传输定理

负载接收的功率量是电气和电子应用中的一个重要参数。在直流电路中，我们可以用电阻为 R_L 欧姆的电阻器来表示负载。类似地，在交流电路中，我们可以用阻抗为 Z_L 欧姆的复负载来表示它。

最大功率传输定理指出，只有当负载电阻等于源电阻时，直流电压源才会向可变负载电阻提供最大功率。

类似地，最大功率传输定理指出，只有当负载阻抗等于源阻抗的复共轭时，交流电压源才会向可变复负载提供最大功率。

在本章中，让我们讨论直流电路的最大功率传输定理。

最大功率传输定理的证明

用戴维南等效电路替换可变负载电阻左侧电阻为 R_L 欧姆的任意两端线性网络或电路。我们知道，戴维南等效电路类似于实际电压源。

下图说明了这一概念。

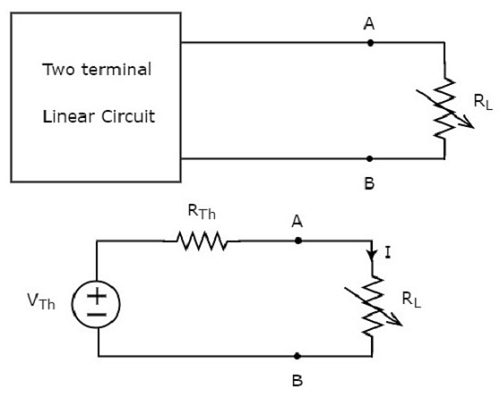
负载电阻上耗散的功率为

$$P_L = I^2 R_L$$

将 $I = \frac{V_{Th}}{R_{Th} + R_L}$ 代入上述公式。

$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} group ^2 R_L$$

$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} brace$ 公式 1

最大功率传输条件

对于最大值或最小值，一阶导数将为零。因此，对公式 1 求 R_L 的导数，使其等于零。

$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 imes 1 - R_L imes 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} brace = 0$$

$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$

$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$

$$\Rightarrow (R_{Th} - R_L) = 0$$

$$\Rightarrow R_{Th} = R_L\:or\:R_L = R_{Th}$$

因此，负载上最大功率耗散的条件是 $R_L = R_{Th}$。这意味着，如果负载电阻的值等于源电阻的值，即戴维南电阻，则负载上耗散的功率将达到最大值。

最大功率传输值

在公式 1 中代入 $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$。

$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} brace$$

$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} brace$$

$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$

$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: 因为 \: R_{L} = R_{Th}$$

因此，传输到负载的最大功率为

$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$

最大功率传输效率

我们可以使用以下公式计算最大功率传输效率$\eta_{Max}$。

$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ 公式 2

其中，

• $P_{L, Max}$ 是传输到负载的最大功率。

• $P_S$ 是源产生的功率。

源产生的功率为

$$P_S = I^2 R_{Th} + I^2 R_L$$

$$\Rightarrow P_S = 2 I^2 R_{Th},\:since\:R_{L} = R_{Th}$$

• 将 $I = \frac{V_{Th}}{2 R_{Th}}$ 代入上述方程式。

$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} group ^2 R_{Th}$$

$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} group R_{Th}$$

$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$

• 将 $P_{L, Max}$ 和 $P_S$ 的值代入方程式 2。

$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} group}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}} group}$$

$$\Rightarrow \eta_{Max} = \frac{1}{2}$$

我们可以用百分比表示最大功率传输的效率，如下所示 −

$$\% \eta_{Max} = \eta_{Max} imes 100\%$$

$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} group imes 100\%$$

$$\Rightarrow \% \eta_{Max} = 50\%$$

因此，最大功率传输效率为 50 %。

示例

求出可传输至下图所示电路的负载电阻 R_L 的最大功率。

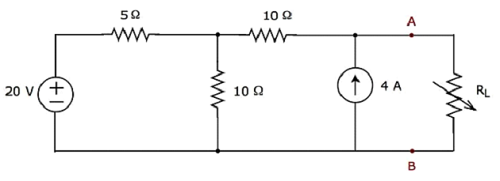
步骤 1 − 在戴维南定理章节中，我们计算了端子 A 和 B 左侧的戴维南等效电路。现在我们可以使用此电路。如下图所示。

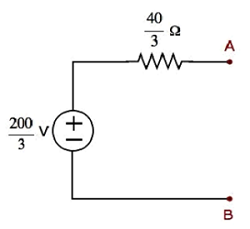
这里，戴维南电压 $V_{Th} = \frac{200}{3}V$ 和戴维南电阻 $R_{Th} = \frac{40}{3} \Omega$

步骤 2 − 将给定电路的端子 A 和 B 左侧的电路部分替换为上述戴维南等效电路。得到的电路图如下图所示。

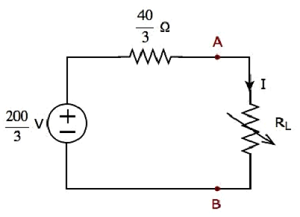
步骤 3 −我们可以使用以下公式找到将传输到负载电阻 R_L 的最大功率。

$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$

在上述公式中代入 $V_{Th} = \frac{200}{3}V$ 和 $R_{Th} = \frac{40}{3} \Omega$。

$$P_{L, Max} = \frac{\lgroup \frac{200}{3} group ^ 2}{4 \lgroup \frac{40}{3} group } $$

$$P_{L, Max} = \frac{250}{3} W$$

因此，将传送到给定电路的负载电阻 RL 的最大功率为 $\mathbf {\frac{250}{3}}$ W