网络理论 - 星型到三角型的转换
在上一章中,我们讨论了三角型网络转换为等效星型网络。现在,让我们讨论星型网络转换为等效三角型网络。这种转换称为星型到三角形转换。
在上一章中,我们从三角形网络得到了星型网络的电阻,如下所示
$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ 公式 1
$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ 公式 2
$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ 公式 3
星型网络电阻与 Delta 网络电阻的关系
我们来操作上述公式,以便根据星型网络电阻获得 Delta 网络电阻。
将两组公式相乘,然后相加。
$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$
$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$
$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4
将方程 4 除以方程 2,我们将得到
$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$
$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
将方程 4 除以方程 3,我们将得到
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
将方程 4 除以方程 1,我们将得到得到
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
利用上述关系,我们可以从星型网络的电阻中找到三角形网络的电阻。这样,我们就可以将星型网络转换为三角形网络。
示例
让我们计算三角形网络的电阻,它相当于星型网络的电阻,如下图所示。
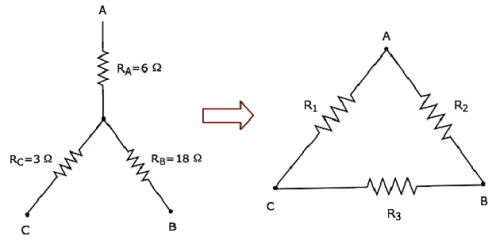
假设星型网络的电阻为RA = 6 Ω、RB = 18 Ω和RC = 3 Ω。
我们知道三角形网络的电阻与星型网络的电阻有以下关系。
$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
将上述方程中的 RA、RB 和 RC 值代入方程中。
$$R_1 = 3 + 6 + \frac{3 imes 6}{18} = 9 + 1 = 10 \Omega$$
$$R_2 = 6 + 18 + \frac{6 imes 18}{3} = 24 + 36 = 60 \Omega$$
$$R_3 = 18 + 3 + \frac{18 imes 3}{6} = 21 + 9 = 30 \Omega$$
因此,我们得到三角形网络的电阻为 R1 = 10 Ω、R2 = 60 Ω 和 R3 = 30 Ω,它们相当于给定星型网络的电阻。


