网络理论 - 三角形到星形转换

在上一章中，我们讨论了一个与等效电阻相关的示例问题。在那里，我们很容易地计算了给定电网端子 A 和 B 之间的等效电阻。因为在每一步中，我们都得到了以串联或并联形式连接的电阻器的组合。

但是，在某些情况下，很难按照以前的方法简化网络。例如，电阻器以三角形 (δ) 形式或星形形式连接。在这种情况下，我们必须转换一种形式的网络为另一种形式，以便通过使用串联组合或并联组合进一步简化它。在本章中，我们将讨论三角形到星形的转换。

三角形网络

考虑以下三角形网络，如下图所示。

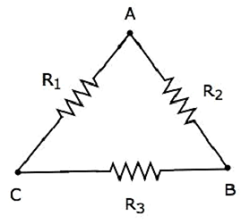
以下方程表示当第三个端子保持开路时，三角形网络两个端子之间的等效电阻。

$$R_{AB} = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$$

$$R_{BC} = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$$

$$R_{CA} = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$$

星型网络

下图显示了与上述三角形网络相对应的等效星型网络。

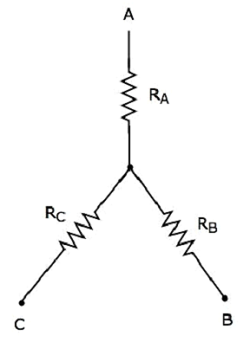
当第三个终端保持开路时，以下方程表示星型网络两个终端之间的等效电阻。

$$R_{AB} = R_A + R_B$$

$$R_{BC} = R_B + R_C$$

$$R_{CA} = R_C + R_A$$

以三角形网络电阻表示的星型网络电阻

我们将通过使公式右侧项相等来得到以下方程上述方程的左边项相同。

$R_A + R_B = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$ 公式 1

$R_B + R_C = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$ 公式 2

$R_C + R_A = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$ 公式3

将上述三个方程相加，我们将得到

$$2(R_A + R_B + R_C) = \frac{2(R_1 R_2 + R_2 R_3 + R_3 R_1)}{R_1 + R_2 + R_3}$$

$\Rightarrow R_A + R_B + R_C = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3}$ 方程 4

从方程 4 中减去方程 2。

$R_A + R_B + R_C - (R_B + R_C) = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3} - \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$

$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$

从公式 4 中减去公式 3，我们将得到

$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$

从公式 4 中减去公式 1，我们将得到

$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$

利用上述关系，我们可以从三角形网络的电阻中找到星型网络的电阻。这样，我们就可以将三角形网络转换为星型网络。

示例

让我们计算星型网络的电阻，它相当于下图所示的三角形网络的电阻。

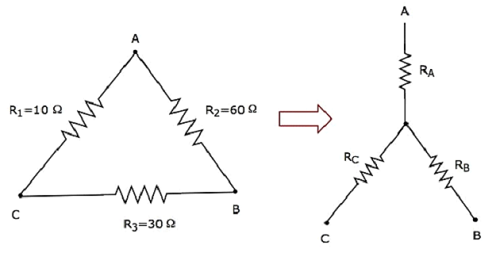
假设三角形网络的电阻为R₁ = 10 Ω，R₂ = 60 Ω并且 R₃ = 30 Ω。

我们知道星型网络的电阻与三角形网络的电阻之间存在以下关系。

$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$

$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$

$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$

将 R₁、R₂ 和 R₃ 的值代入上述方程中。

$$R_A = \frac{10 imes 60}{10 +60+30} = \frac{600}{100} = 6\Omega$$

$$R_B = \frac{60 imes 30}{10 +60+30} = \frac{1800}{100} = 18\Omega$$

$$R_C = \frac{30 imes 10}{10 +60+30} = \frac{300}{100} = 3\Omega$$

因此，我们得到星型网络的电阻为 R_A = 6 Ω、R_B = 18 Ω 和 R_C = 3 Ω，它们相当于给定三角形网络的电阻。