根轨迹的构造

根轨迹是 s 域中的图形表示，它关于实轴对称。因为开环极点和零点存在于 s 域中，其值要么是实数，要么是复数共轭对。在本章中，我们将讨论如何构造（绘制）根轨迹。

根轨迹构造规则

遵循这些规则来构造根轨迹。

规则 1 − 在"s"平面中定位开环极点和零点。

规则 2 − 找到根轨迹分支的数量。

我们知道根轨迹分支从开环极点开始，到开环零点结束。因此，根轨迹分支的数量N等于有限开环极点的数量P或有限开环零点的数量Z，以较大者为准。

从数学上讲，我们可以将根轨迹分支的数量N写为

如果$P\geq Z$，则$N=P$

如果$P<Z$，则$N=Z$

规则 3 − 识别并绘制实轴根轨迹分支。

如果开环传递函数在某点的角度是 180⁰ 的奇数倍，则该点位于根轨迹上。如果实轴上某点左侧有奇数个开环极点和零点，则该点位于根轨迹分支上。因此，满足此条件的点的分支就是根轨迹分支的实轴。

规则 4 − 找到质心和渐近线的角度。

• 如果 $P = Z$，则所有根轨迹分支都从有限开环极点开始，到有限开环零点结束。

• 如果 $P > Z$ ，则 $Z$ 个根轨迹分支从有限开环极点开始，到有限开环零点结束，而 $P − Z$ 个根轨迹分支从有限开环极点开始，到无限开环零点结束。

• 如果 $P < Z$ ，则 P 个根轨迹分支从有限开环极点开始，到有限开环零点结束，而 $Z − P$ 个根轨迹分支从无限开环极点开始，到有限开环零点结束。

因此，当 $P eq Z$ 时，一些根轨迹分支趋近于无穷大。渐近线给出了这些根轨迹分支的方向。实轴上渐近线的交点称为质心。

我们可以使用这个公式计算质心 α，

$\alpha = \frac{\sum Real\: part\: of\: finite\: ​​open\: loop\: polars\:-\sum Real\: part\: of\: finite\: ​​open\: loop\: zeros}{P-Z}$

渐近线 θ 的角度公式为

$$ heta=\frac{(2q+1)180^0}{P-Z}$$

其中，

$$q=0,1,2,....,(P-Z)-1$$

规则 5 −找到根轨迹分支与虚轴的交点。

我们可以使用 Routh 数组方法和特殊情况 (ii)来计算根轨迹分支与虚轴的交点以及该点的 K 值。

• 如果 Routh 数组中任何一行的所有元素均为零，则根轨迹分支与虚轴相交，反之亦然。

• 以这样的方式标识行：如果我们将第一个元素设为零，则整行的元素均为零。找到此组合的 K 值。

• 将此 K 值代入辅助方程中。您将得到根轨迹分支与虚轴的交点。

规则 6 − 找到脱离点和切入点。

• 如果两个开环极点之间存在实轴根轨迹分支，则这两个开环极点之间将有一个脱离点。

• 如果两个开环零点之间存在实轴根轨迹分支，则这两个开环零点之间将有一个切入点。

注意 − 脱离点和切入点仅存在于实轴根轨迹分支上。

按照以下步骤查找脱离点和切入点。

• 根据特征方程 $1 + G(s)H(s) = 0$，以 $s$ 的形式写出 $K$。

• 对 s 微分 $K$ 并使其等于零。将这些 $s$ 值代入上述方程。

• $K$ 值为正的 $s$ 值即为断点。

规则 7 −找到出发角和到达角。

出发角和到达角可以分别在复共轭开环极点和复共轭开环零点处计算。

出发角 $\phi_d$ 的公式为

$$\phi_d=180^0-\phi$$

到达角 $\phi_a$ 的公式为

$$\phi_a=180^0+\phi$$

其中，

$$\phi=\sum \phi_P-\sum \phi_Z$$

示例

现在让我们绘制具有开环传递函数的控制系统的根轨迹， $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$

步骤 1 − 给定的开环传递函数在 $s = 0、s = −1$ 和 $s = −5$ 处有三个极点。它没有任何零点。因此，根轨迹分支的数量等于开环传递函数的极点数量。

$$N=P=3$$

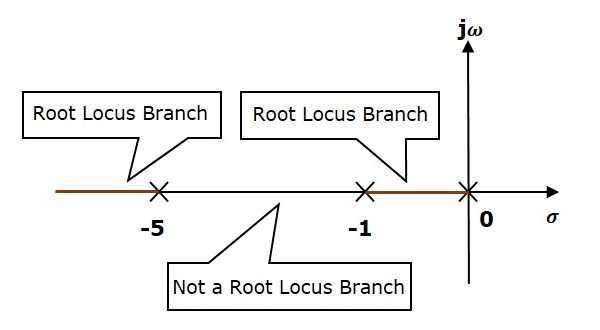
三个极点的位置如上图所示。$s = −1$ 和 $s = 0$ 之间的线段是实轴上根轨迹的一个分支。而根轨迹在实轴上的另一个分支是$s = −5$左边的线段。

步骤2 − 我们将利用给出的公式得到质心和渐近线的角度。

质心 $\alpha = −2$

渐近线的角度为 $ heta = 60^0,180^0$ 和 $300^0$。

下图显示了质心和三条渐近线。

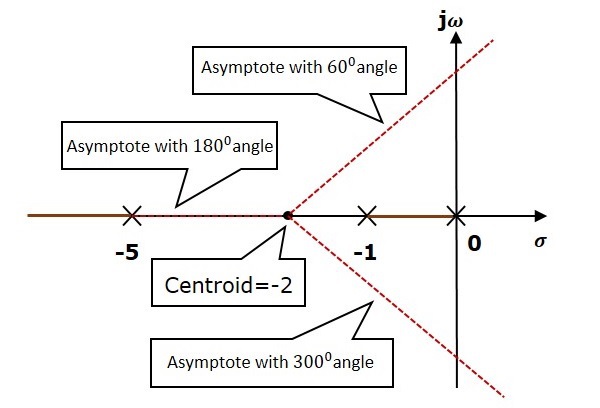
步骤3 − 由于两个渐近线的角度分别为 $60^0$ 和 $300^0$，因此两个根轨迹分支与虚轴相交。利用劳斯阵法和特殊情况(ii)，根轨迹分支与虚轴相交于$j\sqrt{5}$和$−j\sqrt{5}$。

在极点$s = −1$和$s = 0$之间的实轴根轨迹分支上会有一个脱离点。按照给定的计算脱离点的程序，我们将得到 $s = −0.473$。

给定控制系统的根轨迹图如下图所示。

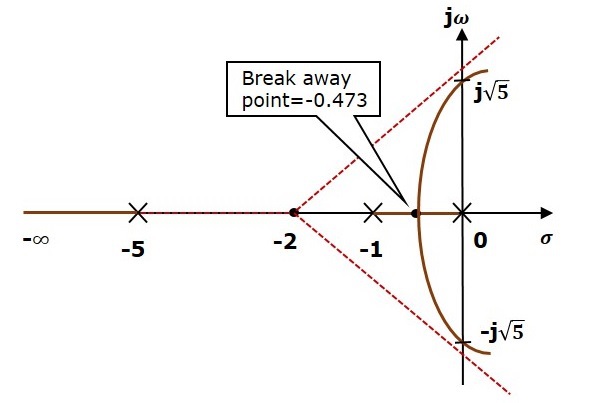
通过这种方式，您可以绘制任何控制系统的根轨迹图，并观察闭环传递函数极点的运动。

从根轨迹图中，我们可以知道不同类型阻尼的 K 值范围。

添加开环极点和零点对根轨迹的影响

通过添加开环极点和开环零点，可以在's'平面中移动根轨迹。

• 如果我们在开环传递函数中包含一个极点，那么一些根轨迹分支将移向's'平面的右半部分。因此，阻尼比$\delta$会减小。这意味着，阻尼频率$\omega_d$会增加，而时间域规范（如延迟时间$t_d$、上升时间$t_r$和峰值时间$t_p$）会减小。但是，它会影响系统的稳定性。

• 如果我们在开环传递函数中包含一个零点，那么一些根轨迹分支将移向's'平面的左半部分。因此，它将增加控制系统的稳定性。在这种情况下，阻尼比$\delta$会增加。这意味着，阻尼频率$\omega_d$会减小，而时间域规范（如延迟时间$t_d$、上升时间$t_r$和峰值时间$t_p$）会增大。

因此，根据要求，我们可以将开环极点或零点包含（添加）到传递函数中。