---

DSP - 快速傅里叶变换

快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

在早期的 DFT 方法中，我们已经看到计算部分太长。我们想减少它。这可以通过 FFT 或快速傅里叶变换来实现。因此，我们可以说 FFT 只不过是以算法格式计算离散傅里叶变换，其中计算部分将减少。

使用 FFT 的主要优点是，通过它，我们可以设计 FIR 滤波器。从数学上讲，FFT 可以写成如下形式；

$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$

让我们举一个例子来更好地理解它。我们考虑了从 $x_0\quad 到 \quad x_7$ 命名的八个点。我们将在一个组中选择偶数项，在另一个组中选择奇数项。上述内容的示意图如下所示 −

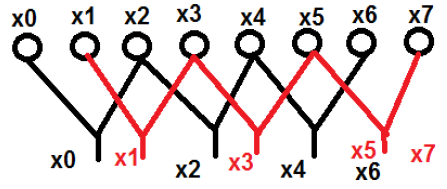
这里，点 x₀、x₂、x₄ 和 x₆ 被分组为一个类别，类似地，点 x₁、x₃、x₅ 和 x₇ 被归入另一个类别。现在，我们可以进一步将它们分成两组并继续计算。现在，让我们看看这些进一步分解成两个如何有助于计算。

$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$

$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk} imes W_N^k$

$= G[k]+H[k] imes W_N^k$

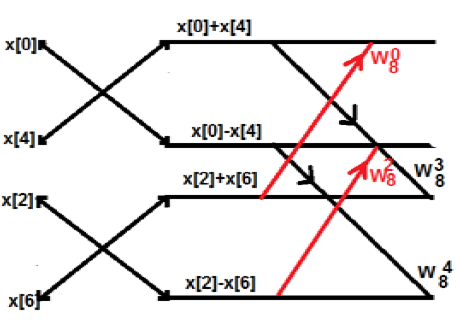
最初，我们取一个八点序列，但后来我们将其分成两部分 G[k] 和 H[k]。G[k] 代表偶数部分，而 H[k] 代表奇数部分。如果我们想通过一个图来实现，那么可以如下图所示 −

从上图我们可以看出

$W_8^4 = -1$

$W_8^5 = -W_8^1$

$W_8^6 = -W_8^2$

$W_8^7 = -W_8^3$

同样，最终值可以写成 −

$G[0]-H[0] = x[4]$

$G[1]-W_8^1H[1] = x[5]$

$G[2]-W_8^2H[2] = x[6]$

$G[1]-W_8^3H[3] = x[7]$

上面是一个周期序列。该系统的缺点是 K 不能在 4 点之后被打破。现在让我们将上面的内容进一步分解。我们将得到类似这样的结构

示例

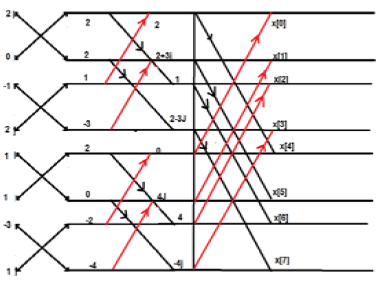
考虑序列 x[n]={ 2,1,-1,-3,0,1,2,1}。计算 FFT。

解决方案 − 给定的序列是 x[n]={ 2,1,-1,-3,0,1,2,1

按如下所示排列项；

---