信号与系统简介
本教程涵盖了理解数字图像处理概念所必需的信号与系统基础知识。在深入讨论详细概念之前,让我们先定义一些简单的术语。
信号
在电气工程中,表示某些信息的基本量称为信号。信息是什么并不重要,即:模拟信息还是数字信息。在数学中,信号是传达某些信息的函数。事实上,任何可通过时间、空间或任何更高维度测量的量都可以视为信号。信号可以是任何维度,也可以是任何形式。
模拟信号
信号可以是模拟量,这意味着它是相对于时间定义的。它是一个连续信号。这些信号是通过连续独立变量定义的。它们很难分析,因为它们带有大量的值。由于有大量的值样本,因此它们非常准确。为了存储这些信号,您需要无限大的内存,因为它可以在实线上实现无限的值。模拟信号用正弦波表示。
例如:
人声
人声是模拟信号的一个例子。当您说话时,产生的声音以压力波的形式在空气中传播,因此属于数学函数,具有空间和时间的独立变量以及与气压相对应的值。
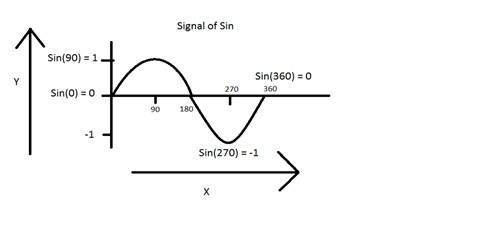
另一个例子是正弦波,如下图所示。
Y = sin(x),其中 x 是独立的
数字信号
与模拟信号相比,数字信号非常容易分析。它们是不连续的信号。它们是模拟信号的占用。
"数字"一词代表离散值,因此意味着它们使用特定值来表示任何信息。在数字信号中,仅使用两个值来表示某些东西,即:1 和 0(二进制值)。数字信号不如模拟信号准确,因为它们是模拟信号在一段时间内采集的离散样本。但是,数字信号不受噪声的影响。因此它们持续时间长且易于解释。数字信号用方波表示。
例如:
计算机键盘
每当从键盘按下一个键时,就会向键盘控制器发送相应的电信号,其中包含该特定键的 ASCII 值。例如,按下键盘键 a 时产生的电信号以 0 和 1 的形式携带数字 97 的信息,这是字符 a 的 ASCII 值。
模拟信号和数字信号之间的区别
| 比较元素 | 模拟信号 | 数字信号 |
|---|---|---|
| 分析 | 困难 | 可以分析 |
| 表示 | 连续 | 不连续 |
| 准确性 | 更准确 | 不太准确 |
| 存储 | 无限内存 | 易于存储 |
| 受噪音 | 是 | 否 |
| 记录技术 | 保留原始信号 | 采集并保存信号样本 |
| 示例 | 人声、温度计、模拟电话等 | 计算机、数字电话、数字笔等 |
系统
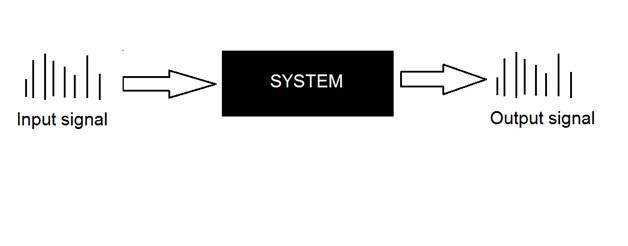
系统由其处理的输入和输出类型定义。由于我们处理的是信号,因此在我们的例子中,我们的系统将是一个数学模型、一段代码/软件、或一个物理设备或一个黑匣子,其输入是信号并对该信号执行一些处理,输出也是信号。输入称为激励,输出称为响应。

上图显示了一个系统,其输入和输出都是信号,但输入是模拟信号。输出是数字信号。这意味着我们的系统实际上是一个将模拟信号转换为数字信号的转换系统。
让我们看看这个黑匣子系统的内部
模拟信号到数字信号的转换
由于有很多概念与这种模拟到数字转换以及反之亦然有关。我们将仅讨论与数字图像处理相关的概念。转换涉及两个主要概念。
- 采样
- 量化
采样
顾名思义,采样可以定义为取样。在 x 轴上对数字信号进行采样。采样是在独立变量上进行的。以这个数学方程为例:

采样是在 x 变量上进行的。我们也可以说,x 轴(无限值)到数字的转换是在采样下完成的。
采样进一步分为上采样和下采样。如果 x 轴上的值范围较小,那么我们将增加值的样本。这称为上采样,反之亦然称为下采样。</p>
量化
顾名思义,量化可以定义为分成量子(分区)。量化是在因变量上进行的。它与采样相反。
在这个数学方程式中,y = sin(x)
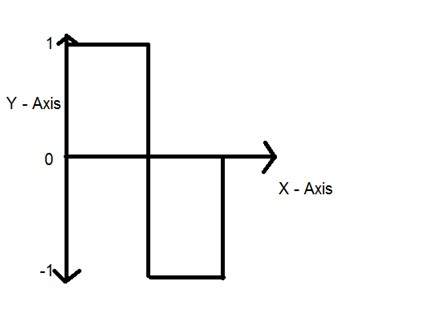
量化是在 Y 变量上进行的。它是在 y 轴上进行的。将 y 轴无限值转换为 1、0、-1(或任何其他级别)称为量化。
这是将模拟信号转换为数字信号时涉及的两个基本步骤。
信号的量化已在下图中显示。
为什么我们需要将模拟信号转换为数字信号。
第一个也是显而易见的原因是数字图像处理处理的是数字图像,即数字信号。因此,无论何时捕获图像,它都会被转换为数字格式,然后进行处理。
第二个也是最重要的原因是,为了使用数字计算机对模拟信号进行操作,您必须将该模拟信号存储在计算机中。而为了存储模拟信号,需要无限的内存来存储它。因为这是不可能的,所以我们将信号转换成数字格式,然后将其存储在数字计算机中,然后对其进行操作。
连续系统与离散系统
连续系统
输入和输出都是连续信号或模拟信号的系统类型称为连续系统。
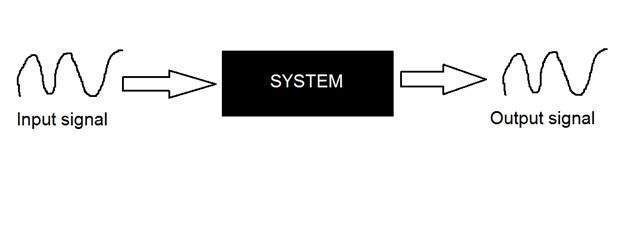
离散系统
输入和输出都是离散信号或数字信号的系统类型称为数字系统。