灰度变换

我们在基本变换教程中讨论了一些基本变换。在本教程中，我们将介绍一些基本的灰度变换。

图像增强

与未增强的图像相比，增强图像可提供更好的对比度和更详细的图像。图像增强有很多应用。它用于增强医学图像、遥感捕获的图像、卫星图像等。

变换函数如下所示

s = T ( r )

其中 r 是输入图像的像素，s 是输出图像的像素。T 是将 r 的每个值映射到 s 的每个值的变换函数。图像增强可以通过下面讨论的灰度变换来完成。

灰度变换

有三种基本的灰度变换。

• 线性
• 对数
• 幂律

这些转换的整体图形如下所示。

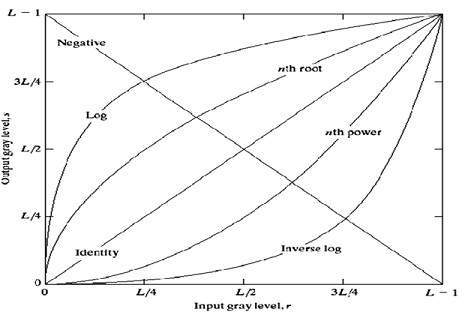
线性变换

首先我们来看看线性变换。线性变换包括简单的恒等变换和负变换。恒等变换在我们的图像变换教程中已经讨论过，但这里只给出了这种变换的简要说明。

恒等变换用直线表示。在这种转换中，输入图像的每个值都直接映射到输出图像的每个其他值。这会产生相同的输入图像和输出图像。因此称为恒等变换。如下所示：

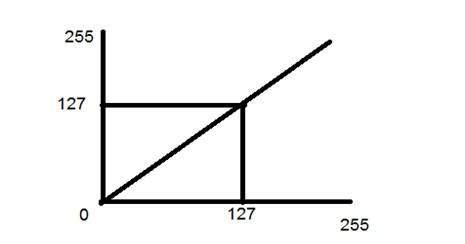
负变换

第二个线性变换是负变换，它是恒等变换的逆。在负变换中，输入图像的每个值都从 L-1 中减去并映射到输出图像上。

结果有点像这样。

输入图像

输出图像

在这种情况下，已完成以下转换。

s = (L – 1) – r

由于爱因斯坦的输入图像是 8 bpp 图像，因此该图像中的级别数为 256。将 256 代入等式，我们得到

s = 255 – r

因此每个值都减去 255，结果图像已显示在上方。因此，发生的事情是，较亮的像素变暗，较暗的图片变亮。并且会导致图像为负片。

如下图所示。

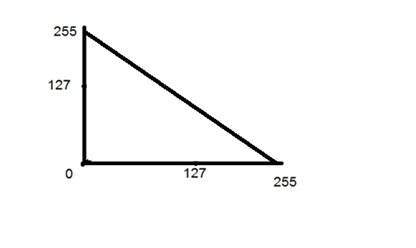
对数变换

对数变换进一步包含两种类型的变换。对数变换和逆对数变换。

对数变换

对数变换可以通过以下公式定义

s = c log(r + 1)。

其中 s 和 r 是输出和输入图像的像素值，c 是常数。将值 1 添加到输入图像的每个像素值，因为如果图像中的像素强度为 0，则 log (0) 等于无穷大。因此添加 1，使最小值至少为 1。

在对数变换期间，与较高像素值相比，图像中的暗像素会扩大。在对数变换中，较高像素值会被压缩。这会导致以下图像增强。

对数变换中的 c 值会调整您要寻找的增强类型。

输入图像

对数变换图像

逆对数变换与对数变换相反。

幂律变换

还有两种变换是幂律变换，包括 n 次方和 n 次方根变换。这些变换可以用以下表达式给出：

s=cr^γ

这个符号 γ 称为伽马，因此这种变换也称为伽马变换。

γ 值的变化会改变图像的增强效果。不同的显示设备/显示器有自己的伽马校正，这就是它们以不同强度显示图像的原因。

这种类型的转换用于增强不同类型的显示设备的图像。不同显示设备的伽马是不同的。例如，CRT 的 Gamma 介于 1.8 到 2.5 之间，这意味着 CRT 上显示的图像是暗的。

校正 Gamma。

s=cr^γ

s=cr^(1/2.5)

此处显示了具有不同 Gamma 值的相同图像。

例如

Gamma = 10

Gamma = 8

Gamma = 6