卷积的概念
本教程是关于信号与系统的一个非常重要的概念。我们将全面讨论卷积。它是什么?为什么是它?我们能用它做什么?
我们将从图像处理的基础开始讨论卷积。
什么是图像处理
正如我们在图像处理教程的介绍和信号与系统中所讨论的那样,图像处理或多或少是信号与系统的研究,因为图像只不过是一个二维信号。
我们还讨论过,在图像处理中,我们正在开发一个系统,其输入是图像,输出也是图像。这可以用图形表示。
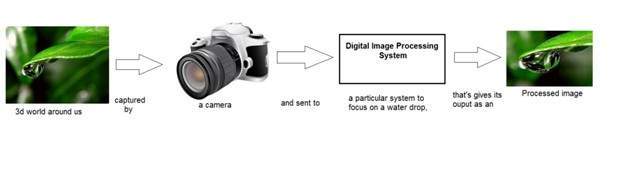
上图中标记为"数字图像处理系统"的框可以被认为是一个黑匣子
它可以更好地表示为:

到目前为止我们到达了哪里
到目前为止,我们已经讨论了两种处理图像的重要方法。或者换句话说,我们可以说,到目前为止,我们的黑匣子以两种不同的方式工作。
处理图像的两种不同方法是
图形(直方图)

这种方法称为直方图处理。我们在之前的教程中详细讨论了它,用于增加对比度、图像增强、亮度等。
变换函数
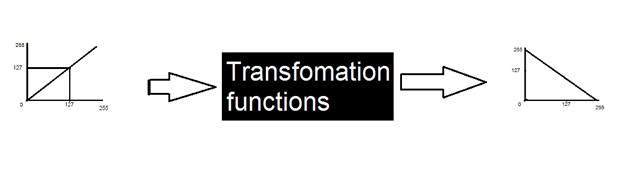
这种方法称为变换,其中我们讨论了不同类型的变换和一些灰度变换
处理图像的另一种方法
在这里我们将讨论另一种处理图像的方法。这种方法称为卷积。通常用于图像处理的黑箱(系统)是 LTI 系统或线性时不变系统。线性是指输出始终为线性的系统,既不是对数也不是指数或任何其他形式。时不变是指随时间保持不变的系统。
所以现在我们将使用第三种方法。它可以表示为。

它可以在数学上表示为两种方式
g(x,y) = h(x,y) * f(x,y)
它可以解释为"与图像卷积的掩码"。
或者
g(x,y) = f(x,y) * h(x,y)
它可以解释为"与掩码卷积的图像"。
有两种表示方法,因为卷积运算符(*)是可交换的。h(x,y)是掩码或过滤器。
什么是掩码?
掩码也是一种信号。它可以用二维矩阵表示。掩码通常为 1x1、3x3、5x5、7x7 的大小。掩码应始终为奇数,否则您将无法找到掩码的中间值。为什么我们需要找到掩码的中间值。答案位于下文中,主题为"如何执行卷积?"
如何进行卷积?
为了对图像进行卷积,应采取以下步骤。
- 仅翻转蒙版(水平和垂直)一次
- 将蒙版滑到图像上。
- 将相应元素相乘,然后添加它们
- 重复此过程,直到计算出图像的所有值。
卷积示例
让我们进行一些卷积。步骤 1 是翻转蒙版。
蒙版
让我们将蒙版设为这个。
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
水平翻转蒙版
| 3 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
垂直翻转蒙版
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
图像
让我们考虑这样的图像
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
卷积
对图像进行卷积掩码。操作如下。将掩码的中心放在图像的每个元素上。将相应的元素相乘然后相加,并将结果粘贴到放置掩码中心的图像元素上。
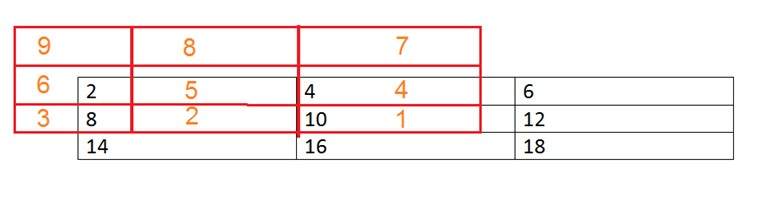
红色框为掩码,橙色中的值是掩码的值。黑色框和值属于图像。现在,对于图像的第一个像素,值将计算为
第一个像素 = (5*2) + (4*4) + (2*8) + (1*10)
= 10 + 16 + 16 + 10
= 52
将 52 放置在原始图像的第一个索引处,并对图像的每个像素重复此过程。
为什么要使用卷积
卷积可以实现前两种处理图像的方法无法实现的功能。这些包括模糊、锐化、边缘检测、降噪等。


