频域简介

我们已经在许多领域处理过图像。现在我们在频域中处理信号（图像）。由于傅里叶级数和频域是纯数学，因此我们将尽量减少数学部分，并将更多精力放在其在 DIP 中的应用上。

频域分析

到目前为止，我们分析信号的所有域都是相对于时间进行分析。但在频域中，我们不相对于时间分析信号，而是相对于频率进行分析。

在空间域中，我们按原样处理图像。图像像素的值会相对于场景而变化。而在频域中，我们处理的是像素值在空间域中变化的速率。

为简单起见，我们这样说。

在简单的空间域中，我们直接处理图像矩阵。而在频域中，我们处理这样的图像。

我们首先将图像转换为其频率分布。然后我们的黑盒系统执行它必须执行的任何处理，在这种情况下，黑盒的输出不是图像，而是一个变换。执行逆变换后，它被转换成图像，然后在空间域中查看。

它可以以图形方式查看为

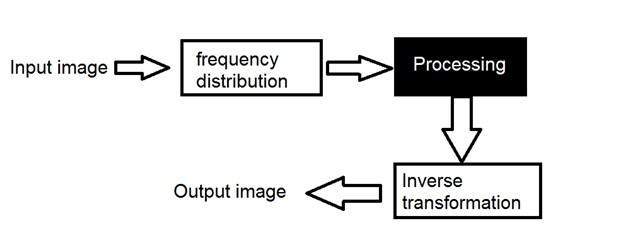
这里我们使用了变换这个词。它实际上是什么意思？

可以使用称为变换的数学运算符将信号从时域转换为频域。有许多种变换可以做到这一点。下面给出了其中一些。

在所有这些中，我们将在下一个教程中彻底讨论傅里叶级数和傅里叶变换。

空间域中的任何图像都可以在频域中表示。但这些频率实际上意味着什么。

我们将频率分量分为两个主要分量。

高频分量对应于图像中的边缘。

图像中的低频分量对应于平滑区域。