卷积定理

在上一篇教程中，我们讨论了频域中的图像。在本教程中，我们将定义频域和图像（空间域）之间的关系。

例如

考虑这个例子。

频域中的同一幅图像可以表示为。

现在图像或空间域与频域之间的关系是什么。这种关系可以通过一个称为卷积定理的定理来解释。

卷积定理

可以通过卷积定理建立空间域和频域之间的关系。

卷积定理可以表示为。

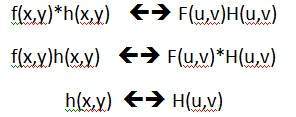
可以说，空间域中的卷积等于频域中的滤波，反之亦然。

频域中的滤波可以表示如下：

滤波步骤如下。

• 第一步，我们必须在空间域中对图像进行一些预处理，即增加其对比度或亮度

• 然后我们将对图像进行离散傅里叶变换

• 然后我们将离散傅里叶变换置于中心，因为我们将把离散傅里叶变换从角落带到中心

• 然后我们将应用过滤，这意味着我们将傅里叶变换乘以过滤函数

• 然后我们再次将 DFT 从中心移到角落

• 最后一步是进行离散傅里叶逆变换，将结果从频域带回到空域

• 后处理这一步是可选的，就像预处理一样，我们只是增加了图像的外观。

过滤器

频域中过滤器的概念与卷积中掩模的概念相同。

将图像转换为频域后，一些过滤器应用于过滤过程，对图像执行不同类型的处理。处理包括模糊图像、锐化图像等。

用于这些目的的常见过滤器类型是：

• 理想高通滤波器
• 理想低通滤波器
• 高斯高通滤波器
• 高斯低通滤波器

在下一个教程中，我们将详细讨论过滤器。