高通与低通滤波器

在上一篇教程中，我们简要讨论了滤波器。在本篇教程中，我们将全面讨论它们。在讨论之前，我们先来谈谈蒙版。在我们的卷积和蒙版教程中已经讨论了蒙版的概念。

模糊蒙版与导数蒙版

我们将对模糊蒙版和导数蒙版进行比较。

模糊蒙版

模糊蒙版具有以下属性。

• 模糊蒙版中的所有值都是正值
• 所有值的总和等于 1
• 使用模糊蒙版可以减少边缘内容
• 随着蒙版尺寸的增大，将产生更多的平滑效果

导数蒙版

导数蒙版具有以下属性。

• 导数蒙版具有正值和负值
• 导数蒙版中的所有值的总和等于零
• 边缘内容通过导数掩码增加
• 随着掩码尺寸的增大，边缘内容也随之增加

高通滤波器和低通滤波器中模糊掩码和导数掩码之间的关系。

高通滤波器和低通滤波器中模糊掩码和导数掩码之间的关系可以简单定义为。

• 模糊掩码也称为低通滤波器
• 导数掩码也称为高通滤波器

高通频率分量和低通频率分量

高通频率分量表示边缘，而低通频率分量表示平滑区域。

理想低通和理想高通滤波器

这是低通滤波器的常见示例。

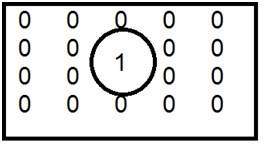
当将 1 放在里面而将 0 放在外面时，我们得到了模糊的图像。现在，随着我们增加 1 的大小，模糊会增加，边缘内容会减少。

这是高通滤波器的常见示例。

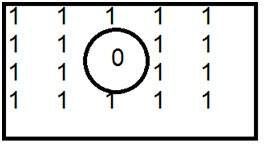
当将 0 放在里面时，我们会得到边缘，这会给我们一个草图图像。下面给出了频域中的理想低通滤波器。

理想的低通滤波器可以图形表示为

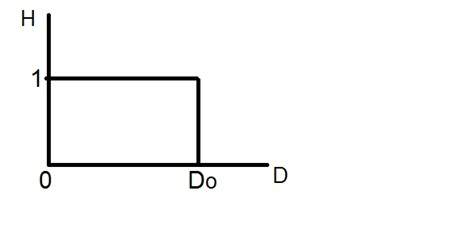
现在让我们将此过滤器应用于实际图像，看看我们得到了什么。

示例图像

频域中的图像

在此图像上应用过滤器

结果图像

使用相同的方法，可以在图像上应用理想的高通滤波器。但显然结果会有所不同，因为低通会减少边缘内容，而高通会增加边缘内容。

高斯低通和高斯高通滤波器

高斯低通和高斯高通滤波器将理想低通和高通滤波器中出现的问题最小化。

这个问题被称为振铃效应。这是因为在某些点上，一种颜色到另一种颜色的过渡无法精确定义，因此在该点会出现振铃效应。

看看这张图。

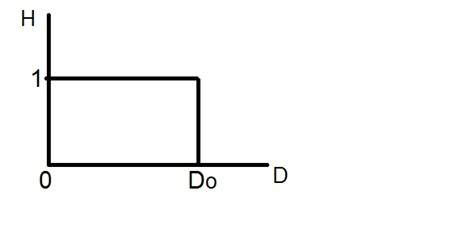
这是理想低通滤波器的表示。现在，在 Do 的确切点，你无法分辨出该值是 0 还是 1。因此，在该点出现了振铃效应。

因此，为了减少理想低通和理想高通滤波器出现的效果，引入了以下高斯低通滤波器和高斯高通滤波器。

高斯低通滤波器

滤波和低通的概念保持不变，但只有过渡变得不同并且变得更加平滑。

高斯低通滤波器可以表示为

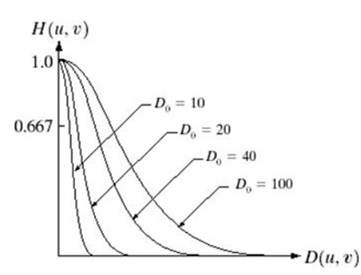
请注意平滑的曲线过渡，因此在每个点都可以精确定义 Do 的值。

高斯高通滤波器

高斯高通滤波器具有与理想高通滤波器相同的概念，但过渡同样更加平滑与理想情况相比。