Z-Transform(Z变换)属性
Z-Transform(Z变换)具有以下属性:
线性属性
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
且 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
则线性属性表明
$a\, x (n) + b\, y (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} a\, X(Z) + b\, Y(Z)$
时间平移属性
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
则时间平移性质表明
$x (n-m) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} z^{-m} X(Z)$
乘以指数序列性质
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
乘以指数序列性质表明
$a^n\, . x(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z/a)$
时间反转性质
如果 $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
则时间反转性质表明
$x (-n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(1/Z)$
Z 域中的微分或乘以 n 性质
如果 $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
则乘以 n 或在 z 域中的微分性质表明
$ n^k x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} [-1]^k z^k{d^k X(Z) \over dZ^K} $
卷积属性
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
且 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
则卷积属性表明
$x(n) * y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z)$
相关性属性
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
且 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
则相关属性表明
$x(n) \otimes y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z^{-1})$
初值和终值定理
针对因果信号定义了 z 变换的初值和终值定理。
初值定理
对于因果信号 x(n),初值定理指出
$ x (0) = \lim_{z o \infty }X(z) $
这用于在不进行逆 z 变换的情况下找到信号的初始值
最终值定理
对于因果信号 x(n),最终值定理指出
$ x ( \infty ) = \lim_{z o 1} [z-1] X(z) $
这用于在不进行逆 z 变换的情况下找到信号的最终值。
Z 变换的收敛区域 (ROC)
z 变换收敛的 z 的变化范围称为收敛区域z 变换。
Z 变换的 ROC 属性
z 变换的 ROC 用 z 平面中的圆圈表示。
ROC 不包含任何极点。
如果 x(n) 是有限持续时间因果序列或右侧序列,则 ROC 是除 z = 0 之外的整个 z 平面。
如果 x(n) 是有限持续时间反因果序列或左侧序列,则 ROC 是除 z = ∞ 之外的整个 z 平面。
如果 x(n) 是无限持续时间因果序列,则 ROC 在半径为 a 的圆的外部。即 |z| > a。
如果 x(n) 是无限持续时间反因果序列,则 ROC 在半径为 a 的圆的内部。即 |z| < a.
如果 x(n) 是有限持续时间的双面序列,则 ROC 是整个 z 平面,除了 z = 0 和 z = ∞。
ROC 的概念可以通过以下示例解释:
示例 1: 查找 $a^n u[n] + a^{-}nu[-n-1]$ 的 z 变换和 ROC
$Z.T[a^n u[n]] + Z.T[a^{-n}u[-n-1]] = {Z \over Z-a} + {Z \over Z {-1 \over a}}$
$$ ROC:|z| \gt a \quad\quad ROC:|z| \lt {1 \over a} $$
ROC 图有两个条件,即 a > 1 和 a < 1,因为您不知道 a。
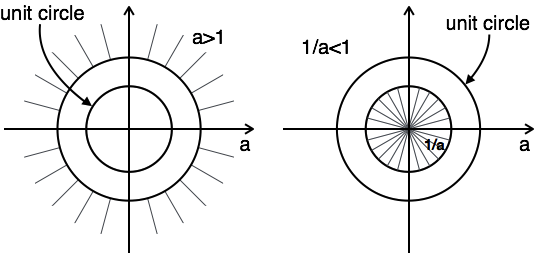
在这种情况下,没有组合 ROC。

这里,ROC 的组合来自 $a \lt |z| \lt {1 \over a}$
因此,对于这个问题,当 a < 时,z 变换是可能的1.
因果关系和稳定性
离散时间 LTI 系统的因果关系条件如下:
离散时间 LTI 系统在以下情况下是因果的
ROC 位于最外层极点之外。
在传递函数 H[Z] 中,分子的阶不能大于分母的阶。
离散时间 LTI 系统的稳定性条件
离散时间 LTI 系统在以下情况下是稳定的
其系统函数 H[Z] 包括单位圆 |z|=1。
传递函数的所有极点均位于单位圆 |z|=1 内。
基本信号的 Z 变换
| x(t) | X[Z] |
|---|---|
| $\delta$ | 1 |
| $u(n)$ | ${Z\over Z-1}$ |
| $u(-n-1)$ | $ -{Z\over Z-1}$ |
| $\delta(n-m)$ | $z^{-m}$ |
| $a^n u[n]$ | ${Z \over Z-a}$ |
| $a^n u[-n-1]$ | $- {Z \over Z-a}$ |
| $n\,a^n u[n]$ | ${aZ \over |Z-a|^2}$ |
| $n\,a^n u[-n-1] $ | $- {aZ \over |Z-a|^2}$ |
| $a^n \cos \omega n u[n] $ | ${Z^2-aZ \cos \omega \over Z^2-2aZ \cos \omega +a^2}$ |
| $a^n \sin \omega n u[n] $ | $ {aZ \sin \omega \over Z^2 -2aZ \cos \omega +a^2 } $ |


