收敛区域 (ROC)
拉普拉斯变换收敛的 σ 范围变化称为收敛区域。
拉普拉斯变换的 ROC 属性
ROC 包含 s 平面中与 jω 轴平行的带状线。
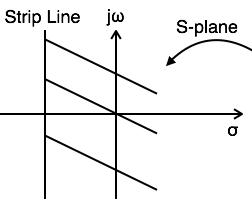
如果 x(t) 是绝对积分并且持续时间有限,则 ROC 是整个 s 平面。
如果 x(t) 是右侧序列,则 ROC : Re{s} > σo.
如果 x(t) 是左侧序列,则 ROC : Re{s} < σo。
如果 x(t) 是双边序列,则 ROC 是两个区域的组合。
可以使用以下示例来解释 ROC:
示例 1:查找 $x(t) = e-^{at}u(t)$ 的拉普拉斯变换和 ROC
$L.T[x(t)] = L.T[e-^{at}u(t)] = {1 \over S+a}$
$ Re{} \gt -a $
$ ROC:Re{s} \gt >-a$
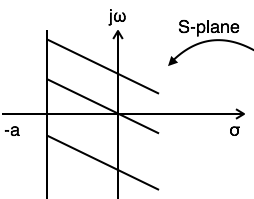
示例 2:查找 $x(t) = e^{at}u(-t)$ 的拉普拉斯变换和 ROC
$ L.T[x(t)] = L.T[e^{at}u(t)] = {1 \over S-a} $
$ Re{s} < a $
$ ROC:Re{s} < a $
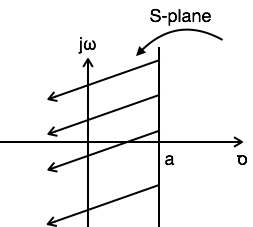
示例 3:查找 $x(t) = e^{-at}u(t)+e^{at}u(-t)$ 的拉普拉斯变换和 ROC
$L.T[x(t)] = L.T[e^{-at}u(t)+e^{at}u(-t)] = {1 \over S+a} + {1 \over S-a}$
对于 ${1 \over S+a} Re\{s\} \gt -a $
对于 ${1 \over S-a} Re\{s\} \lt a $
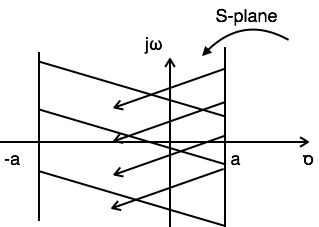
参照上图,组合区域位于-a到a之间。因此,
$ ROC: -a < Re{s} < a $
因果关系和稳定性
对于因果系统,其传递函数的所有极点都必须位于 s 平面的右半部分。
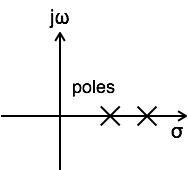
当系统的传递函数的所有极点都位于 s 平面的左半部分时,系统即为稳定系统。
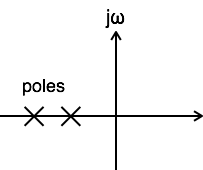
当系统的传递函数中至少有一个极点移至 s 平面的右半部分时,系统即为不稳定系统。
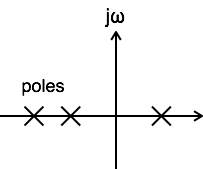
当系统的传递函数至少有一个极点位于 s 平面的 jω 轴上时,系统即为边缘稳定系统。
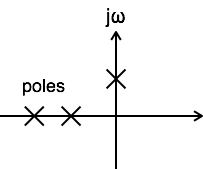
基本函数的 ROC
| f(t) | F(s) | ROC |
|---|---|---|
| $u(t)$ | $${1\over s}$$ | ROC: Re{s} > 0 |
| $ t\, u(t) $ | $${1\over s^2} $$ | ROC:Re{s} > 0 |
| $ t^n\, u(t) $ | $$ {n! \over s^{n+1}} $$ | ROC:Re{s} > 0 |
| $ e^{at}\, u(t) $ | $$ {1\over s-a} $$ | ROC:Re{s} > a |
| $ e^{-at}\, u(t) $ | $$ {1\over s+a} $$ | ROC:Re{s} > -a |
| $ e^{at}\, u(t) $ | $$ - {1\over s-a} $$ | ROC:Re{s} < a |
| $ e^{-at}\, u(-t) $ | $$ - {1\over s+a} $$ | ROC:Re{s} < -a |
| $ t\, e^{at}\, u(t) $ | $$ {1 \over (s-a)^2} $$ | ROC:Re{s} > a |
| $ t^{n} e^{at}\, u(t) $ | $$ {n! \over (s-a)^{n+1}} $$ | ROC:Re{s} > a |
| $ t\, e^{-at}\, u(t) $ | $$ {1 \over (s+a)^2} $$ | ROC:Re{s} > -a |
| $ t^n\, e^{-at}\, u(t) $ | $${n! \over (s+a)^{n+1}} $$ | ROC:Re{s} > -a |
| $ t\, e^{at}\, u(-t) $ | $$ - {1 \over (s-a)^2} $$ | ROC:Re{s} < a |
| $ t^n\, e^{at}\, u(-t) $ | $$ - {n! \over (s-a)^{n+1}} $$ | ROC:Re{s} < a |
| $ t\, e^{-at}\,u(-t) $ | $$ - {1 \over (s+a)^2} $$ | ROC:Re{s} < -a |
| $ t^n\, e^{-at}\, u(-t) $ | $$ - {n! \over (s+a)^{n+1}} $$ | ROC:Re{s} < -a |
| $ e^{-at} \cos \, bt $ | $$ {s+a \over (s+a)^2 + b^2 } $$ | |
| $ e^{-at} \sin\, bt $ | $$ {b \over (s+a)^2 + b^2 } $$ |


