傅里叶变换

傅里叶级数的主要缺点是它只适用于周期信号。有些自然产生的信号，如非周期或非周期信号，我们无法用傅里叶级数来表示。为了克服这一缺点，傅里叶开发了一个数学模型，用于将信号在时间（或空间）域和频域之间进行变换，这被称为"傅里叶变换"。

傅里叶变换在物理学和工程学中有许多应用，例如 LTI 系统分析、雷达、天文学、信号处理等。

从傅里叶级数推导傅里叶变换

考虑一个周期为 T 的周期信号 f(t)。f(t) 的复数傅里叶级数表示如下

$$ f(t) = \sum_{k=-\infty}^{\infty} a_k e^{jk\omega_0 t} $$

$$ \quad \quad \quad \quad \quad = \sum_{k=-\infty}^{\infty} a_k e^{j {2\pi \over T_0} kt} ... ... (1) $$

设 ${1 \over T_0} = \Delta f$，则方程 1 变为

$f(t) = \sum_{k=-\infty}^{\infty} a_k e^{j2\pi k \Delta ft} ... ... (2) $

但你知道

$a_k = {1\over T_0} \int_{t_0}^{t_0+T} f(t) e^{-j k\omega_0 t} dt$

代入方程 2。

(2) $ \Rightarrow f(t) = \Sigma_{k=-\infty}^{\infty} {1 \over T_0} \int_{t_0}^{t_0+T} f(t) e^{-j k\omega_0 t} dt\, e^{j2\pi k \Delta ft} $

设 $t_0={T\over2}$

$ = \Sigma_{k=-\infty}^{\infty} [ \int_{-T\over2}^{T\over2} f(t) e^{-j2 \pi k \Delta ft} dt ] \, e^{j2 \pi k \Delta ft}.\Delta f $

在极限情况下，当 $T o \infty 时，\Delta f$ 趋近于微分 $df，k \Delta f$ 变为连续变量 $f$，求和变为积分

$$ f(t) = lim_{T o \infty} ⁡\left\{ \Sigma_{k=-\infty}^{\infty} [ \int_{-T\over2}^{T\over2} f(t) e^{-j2 \pi k \Delta ft} dt ] \, e^{j2 \pi k \Delta ft}.\Delta f ight\} $$

$$ = \int_{-\infty}^{\infty} [ \int_{-\infty}^{\infty}\,f(t) e^{-j2\pi ft} dt] e^{j2\pi ft} df $$

$$f(t) = \int_{-\infty}^{\infty}\, F[\omega] e^{j\omega t} d \omega$$

$ ext{其中}\,F[\omega] = [ \int_{-\infty}^{\infty}\, f(t) e^{-j2 \pi ft} dt]$

基本函数的傅里叶变换

让我们来看看基本函数的傅里叶变换：

GATE 函数的傅里叶变换

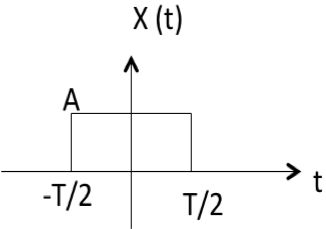
$$F[\omega] = AT Sa({\omega T \over 2})$$

脉冲函数的傅里叶变换

$FT [\omega(t) ] = [\int_{- \infty}^{\infty} \delta (t) e^{-j\omega t} dt] $

$\quad \quad \quad \quad = e^{-j\omega t}\, |\, t = 0 $

$\quad \quad \quad \quad = e^{0} = 1 $

$\quad 因此 \delta (\omega) = 1 $

单位阶跃函数的 FT：

$U(\omega) = \pi \delta (\omega)+1/j\omega$

指数的 FT

$ e^{-at}u(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} 1/(a+jω)$

$ e^{-at}u(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} 1/(a+j\omega )$

$ e^{-a\,|\,t\,|} \stackrel{\mathrm{F.T}}{\longleftrightarrow} {2a \over {a^2+ω^2}}$

$ e^{j \omega_0 t} \stackrel{\mathrm{F.T}}{\longleftrightarrow} \delta (\omega - \omega_0)$

符号函数的傅立叶变换

$ sgn(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} {2 \over j \omega }$

傅里叶变换存在的条件变换

任何函数 f(t) 仅当满足狄利克雷条件时才可以用傅里叶变换表示。即

• 函数 f(t) 具有有限个最大值和最小值。

• 在给定的时间间隔内，信号 f(t) 中必须有有限个不连续点。

• 它必须在给定的时间间隔内绝对可积，即

  $ \int_{-\infty}^{\infty}\, |\, f(t) | \, dt < \infty $

离散时间傅里叶变换 (DTFT)

离散时间傅里叶变换 (DTFT) 或离散时间序列 x[n] 的傅里叶变换是该序列以复指数序列 $e^{j\omega n}$ 表示。

DTFT 序列 x[n] 由以下公式给出

$$ X(\omega) = \Sigma_{n= -\infty}^{\infty} x(n)e^{-j \omega n} \,\, ...\,... (1) $$

这里，X(ω) 是实频率变量 ω 的复函数并且可以写成

$$ X(\omega) = X_{re}(\omega) + jX_{img}(\omega) $$

其中 X_re(ω)、X_img(ω) 分别是 X(ω) 的实部和虚部。

$$ X_{re}(\omega) = |\, X(\omega) | \cos heta(\omega) $$

$$ X_{img}(\omega) = |\, X(\omega) | \sin heta(\omega) $$

$$ |X(\omega) |^2 = |\, X_{re} (\omega) |^2+ |\,X_{im} (\omega) |^2 $$

而X(ω)也可以表示为 $ X(\omega) = |\,X(\omega) | e^{j heta (ω)} $

其中 $ heta(\omega) = arg{X(\omega) } $

$|\,X(\omega) |, heta(\omega)$称为X(ω)的幅度谱和相位谱。

离散时间傅里叶逆变换

$$ x(n) = { 1 \over 2\pi} \int_{-\pi}^{\pi} X(\omega) e^{j \omega n} d\omega \,\, ...\,... (2)$$

收敛条件：

公式 1 中的无穷级数可能收敛，也可能不收敛。x(n) 是绝对可和的。

$$ ext{when}\,\, \sum_{n=-\infty}^{\infty} |\, x(n)|\, < \infty $$

绝对可和序列始终具有有限能量，但有限能量序列不一定是绝对可和的。