卷积和相关性
卷积
卷积是一种数学运算,用于表达 LTI 系统的输入和输出之间的关系。它将 LTI 系统的输入、输出和脉冲响应关联为
$$ y (t) = x(t) * h(t) $$
其中 y (t) = LTI 的输出
x (t) = LTI 的输入
h (t) = LTI 的脉冲响应
卷积有两种类型:
连续卷积
离散卷积
连续卷积

$ y(t) \,\,= x (t) * h (t) $
$= \int_{-\infty}^{\infty} x( au) h (t- au)d au$
(或)
$= \int_{-\infty}^{\infty} x(t - au) h ( au)d au $
离散卷积

$y(n)\,\,= x (n) * h (n)$
$= \Sigma_{k = - \infty}^{\infty} x(k) h (n-k) $
(或)
$= \Sigma_{k = - \infty}^{\infty} x(n-k) h (k) $
通过使用卷积,我们可以找到系统的零状态响应。
反卷积
反卷积是卷积的逆过程,广泛应用于信号和图像处理。
卷积的性质
交换律
$ x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t) $
分配律
$ x_1 (t) * [x_2 (t) + x_3 (t) ] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$
结合律
$x_1 (t) * [x_2 (t) * x_3 (t) ] = [x_1 (t) * x_2 (t)] * x_3 (t) $
移位属性
$ x_1 (t) * x_2 (t) = y (t) $
$ x_1 (t) * x_2 (t-t_0) = y (t-t_0) $
$ x_1 (t-t_0) * x_2 (t) = y (t-t_0) $
$ x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1) $
带脉冲的卷积
$ x_1 (t) * \delta (t) = x(t) $
$ x_1 (t) * \delta (t- t_0) = x(t-t_0) $
单位步长卷积
$ u (t) * u (t) = r(t) $
$ u (t-T_1) * u (t-T_2) = r(t-T_1-T_2) $
$ u (n) * u (n) = [n+1] u(n) $
缩放属性
如果 $x (t) * h (t) = y (t) $
则 $x (a t) * h (a t) = {1 \over |a|} y (a t)$
输出微分
如果 $y (t) = x (t) * h (t)$
则 $ {dy (t) \over dt} = {dx(t) \over dt} * h (t) $
或
$ {dy (t) \over dt} = x (t) * {dh(t) \over dt}$
注意:
两个因果序列的卷积是因果的。
两个反因果序列的卷积是反因果的。
两个长度不等的矩形的卷积产生一个梯形。
两个长度相等的矩形的卷积产生一个三角形。
一个函数的卷积等于该函数的积分。
示例:您知道 $u(t) * u(t) = r(t)$
根据上述说明,$u(t) * u(t) = \int u(t)dt = \int 1dt = t = r(t)$
在这里,您只需积分即可获得结果$u(t)$。
卷积信号的极限
如果两个信号卷积,则得到的卷积信号具有以下范围:
下限之和 < t < 上限之和
例如:找到下面给出的信号卷积范围

这里,我们有两个长度不等的矩形要卷积,结果是一个梯形。
卷积信号的范围是:
下限之和 < t < 上限之和
$-1+-2 < t < 2+2 $
$-3 < t < 4 $
因此结果是周期为 7 的梯形。
卷积信号的面积
卷积信号的面积由 $A_y = A_x A_h$ 给出
其中 Ax = 输入信号下的面积
Ah = 脉冲响应下的面积
Ay = 输出信号下的面积
证明: $y(t) = \int_{-\infty}^{\infty} x( au) h (t- au)d au$
对两边进行积分
$ \int y(t)dt \,\,\, =\int \int_{-\infty}^{\infty}\, x ( au) h (t- au)d au dt $
$ =\int x ( au) d au \int_{-\infty}^{\infty}\, h (t- au) dt $
我们知道任何信号的面积都是该信号本身的积分。
$ 因此 A_y = A_x\,A_h$
直流分量
任何信号的直流分量由
$ ext{直流分量}={ ext{信号面积} \over ext{信号周期}}$
例如:下面给出的结果卷积信号的直流分量是多少?

这里 x1(t) 的面积 = 长度 × 宽度 = 1 × 3 = 3
x2(t) 的面积 = 长度 × 宽度 = 1 × 4 = 4
卷积信号的面积 = x1(t) 的面积 × x2(t) 的面积
= 3 × 4 = 12
卷积信号的持续时间 = 下限之和 < t < 上限之和
= -1 + -2 < t < 2+2
= -3 < t < 4
周期=7
$因此$卷积信号的Dc分量=$ext{信号面积}\overext{信号周期}$
Dc分量=${12\over7}$
离散卷积
让我们看看如何计算离散卷积:
i. 计算离散线性卷积:
卷积两个序列x[n] = {a,b,c} & h[n] = [e,f,g]

卷积输出 = [ ea, eb+fa, ec+fb+ga, fc+gb, gc]
注意:如果任何两个序列分别有 m、n 个样本,那么得到的卷积序列将有 [m+n-1] 个样本。
示例: 卷积两个序列 x[n] = {1,2,3} & h[n] = {-1,2,2>

卷积输出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]
= [-1, 0, 3, 10, 6]
这里 x[n] 包含 3 个样本,h[n] 也有 3 个样本,因此结果序列有 3+3-1 = 5 个样本。
ii. 计算周期或循环卷积:
周期卷积适用于离散傅里叶变换。要计算周期卷积,所有样本都必须是实数。周期性或循环卷积也称为快速卷积。
如果使用循环卷积对长度分别为 m、n 的两个序列进行卷积,则得到的序列具有最大 [m,n] 个样本。
例如:使用循环卷积对两个序列 x[n] = {1,2,3} & h[n] = {-1,2,2} 进行卷积

普通卷积输出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]。
= [-1, 0, 3, 10, 6]
这里 x[n] 包含 3 个样本,h[n] 也包含 3 个样本。因此,循环卷积得到的结果序列必须有 max[3,3]= 3 个样本。
现在要获得周期性卷积结果,正常卷积的前 3 个样本(因为周期为 3)相同,接下来的两个样本添加到第一个样本,如下所示:
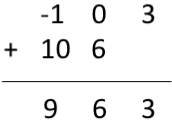
$ 因此$ 循环卷积结果 $y[n] = [9\quad 6\quad 3 ]$
相关性
相关性是两个信号之间相似度的度量。相关性的一般公式是
$$ \int_{-\infty}^{\infty} x_1 (t)x_2 (t- au) dt $$
相关性有两种类型:
自相关
交叉相关
自相关函数
它被定义为信号与自身的相关性。自相关函数是信号与其时间延迟版本之间相似性的度量。它用 R($ au$) 表示。
考虑一个信号 x(t)。 x(t) 及其时间延迟版本的自相关函数由以下公式给出
$$ R_{11} ( au) = R ( au) = \int_{-\infty}^{\infty} x(t)x(t- au) dt \quad \quad ext{[+ve shift]} $$
$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t)x(t + au) dt \quad \quad ext{[-ve shift]} $$
其中 $ au$ = 搜索或扫描或延迟参数。
如果信号复杂,则自相关函数由以下公式给出
$$ R_{11} ( au) = R ( au) = \int_{-\infty}^{\infty} x(t)x * (t- au) dt \quad \quad ext{[+ve shift]} $$
$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t + au)x * (t) dt \quad \quad ext{[-ve shift]} $$
能量信号自相关函数的性质
自相关表现出共轭对称性,即 R ($ au$) = R*(-$ au$)
能量信号在原点即 $ au$=0 处的自相关函数等于该信号的总能量,如下所示:
R (0) = E = $ \int_{-\infty}^{\infty}\,|\,x(t)\,|^2\,dt $
自相关函数 $\infty {1 \over au} $,
自相关函数在 $ au$=0 处最大,即 |R ($ au$) | ≤ R (0) ∀ $ au$
自相关函数和能量谱密度是傅里叶变换对。即
$F.T\,[ R ( au) ] = \Psi(\omega)$
$\Psi(\omega) = \int_{-\infty}^{\infty} R ( au) e^{-j\omega au} d au$
$ R ( au) = x ( au)* x(- au) $
功率信号的自相关函数
周期为 T 的周期功率信号的自相关函数由下式给出
$$ R ( au) = \lim_{T o \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x* (t- au) dt $$
属性
功率信号的自相关表现出共轭对称性,即 $ R ( au) = R*(- au)$
功率信号的自相关函数在 $ au = 0$(在原点)等于该信号的总功率。即
$R (0)= ho $
功率信号的自相关函数 $\infty {1 \over au}$,
功率信号的自相关函数在 $ au$ = 0 时最大,即
$ | R ( au) | \leq R (0)\, \forall \, au$
自相关函数和功率谱密度是傅里叶变换对。即,
$F.T[ R ( au) ] = s(\omega)$
$s(\omega) = \int_{-\infty}^{\infty} R ( au) e^{-j\omega au} d au$
$R ( au) = x ( au)* x(- au) $
密度谱
让我们看看密度谱:
能量密度谱
能量密度谱可以使用以下公式计算:
$$ E = \int_{-\infty}^{\infty} |\,x(f)\,|^2 df $$
功率密度谱
功率密度谱可以使用以下公式计算:
$$P = \Sigma_{n = -\infty}^{\infty}\, |\,C_n |^2 $$
互相关函数
互相关是两个不同信号之间相似度的度量。
考虑两个信号x1(t) 和 x2(t)。这两个信号 $R_{12}( au)$ 的互相关由下式给出
$$R_{12} ( au) = \int_{-\infty}^{\infty} x_1 (t)x_2 (t- au)\, dt \quad \quad ext{[+ve shift]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+ au)x_2 (t)\, dt \quad \quad ext{[-ve shift]}$$
如果信号是复数,则
$$R_{12} ( au) = \int_{-\infty}^{\infty} x_1 (t)x_2^{*}(t- au)\, dt \quad \quad ext{[+ve shift]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+ au)x_2^{*} (t)\, dt \quad \quad ext{[-ve shift]}$$
$$R_{21} ( au) = \int_{-\infty}^{\infty} x_2 (t)x_1^{*}(t- au)\, dt \quad \quad ext{[+ve shift]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_2 (t+ au)x_1^{*} (t)\, dt \quad \quad ext{[-ve shift]}$$
能量和功率信号的互相关函数的性质
自相关表现出共轭对称性,即 $R_{12} ( au) = R^*_{21} (- au)$。
互相关不像卷积那样具有交换性,即
$$ R_{12} ( au) eq R_{21} (- au) $$
-
如果 R12(0) = 0 意味着,如果 $ \int_{-\infty}^{\infty} x_1 (t) x_2^* (t) dt = 0$,则这两个信号被称为正交。
对于功率信号,如果 $ \lim_{T o \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x^* (t)\,dt $,则两个信号被称为正交。
互相关函数对应于一个信号的频谱与另一个信号的频谱的复共轭相乘。即
$$ R_{12} ( au) \leftarrow ightarrow X_1(\omega) X_2^*(\omega)$$
这也称为相关定理。
Parseval 定理
Parseval 能量信号定理指出,信号的总能量可以通过信号的频谱获得,如下所示
$ E = {1\over 2 \pi} \int_{-\infty}^{\infty} |X(\omega)|^2 d\omega $
注意:如果信号具有能量 E,则该信号的时间缩放版本 x(at) 具有能量 E/a。


