幅度调制
连续波连续不断,没有任何间隔,它是包含信息的基带消息信号。该波必须进行调制。
根据标准定义,"载波信号的幅度根据调制信号的瞬时幅度而变化。"这意味着,不包含信息的载波信号的幅度在每个瞬间都根据包含信息的信号的幅度而变化。以下图表可以很好地解释这一点。
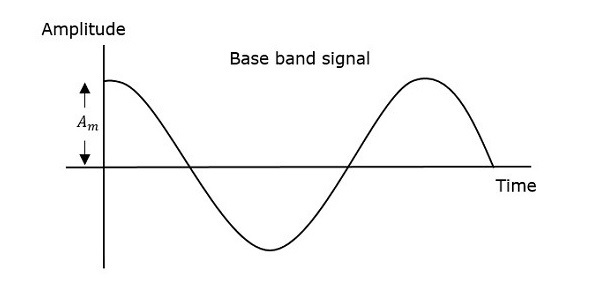
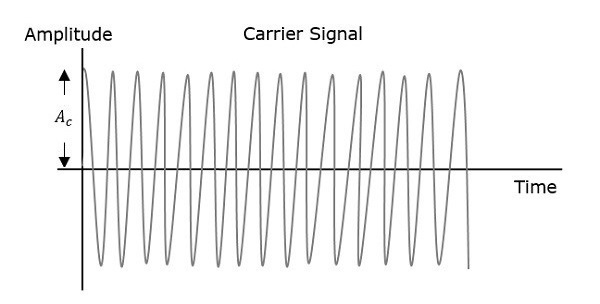
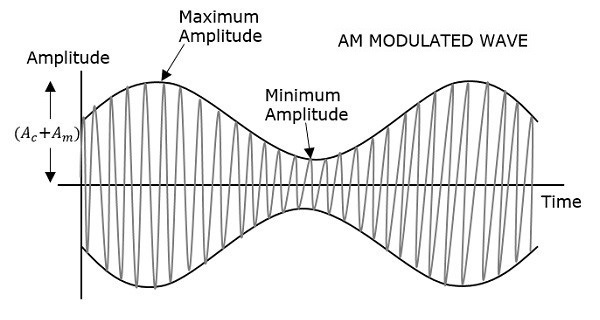
第一个图表显示的是调制波,即消息信号。下一个图表显示的是载波,即高频信号,不包含任何信息。最后一个图表显示的是调制波。
可以观察到,载波的正峰值和负峰值通过一条虚线相互连接。这条线有助于重现调制信号的精确形状。载波上的这条假想线称为包络。它与消息信号的相同。
数学表达式
以下是这些波的数学表达式。
波的时域表示
设调制信号为,
$$m\left ( t ight )=A_m\cos\left ( 2\pi f_mt ight )$$
载波信号为,
$$c\left ( t ight )=A_c\cos\left ( 2\pi f_ct ight )$$
其中,
$A_m$和$A_c$分别是调制信号和载波信号的幅度。
$f_m$和$f_c$是调制信号的频率信号和载波信号。
那么,幅度调制波的方程将是
$s(t)= \left [ A_c+A_m\cos\left ( 2\pi f_mt ight ) ight ]\cos \left ( 2\pi f_ct ight )$ (方程式 1)
调制指数
载波在经过调制后,如果计算出调制水平,则这种尝试称为调制指数或调制深度。它表示载波经历的调制水平。
将公式 1 重新排列如下。
$s(t)=A_c\left [ 1+\left ( \frac{A_m}{A_c} ight )\cos \left ( 2\pi f_mt ight ) ight ]\cos \left ( 2\pi f_ct ight )$
$\Rightarrow s\left ( t ight ) = A_c\left [ 1 + \mu \cos \left ( 2 \pi f_m t ight ) ight ] \cos\left ( 2 \pi f_ct ight )$(公式 2)
其中,$\mu$ 表示调制指数,它等于 $A_m$ 和 $A_c$ 的比率。从数学上讲,我们可以将其写成
$\mu = \frac{A_m}{A_c}$ (公式 3)
因此,当消息和载波信号的幅度已知时,我们可以利用上述公式计算调制指数的值。
现在,让我们通过考虑公式 1 推导出调制指数的另一个公式。当调制波的最大和最小幅度已知时,我们可以使用此公式计算调制指数值。
令 $A_\max$ 和 $A_\min$ 分别为调制波的最大和最小振幅。
当 $\cos \left ( 2\pi f_mt ight )$ 为 1 时,我们将得到调制波的最大振幅。
$\Rightarrow A_\max = A_c + A_m$ (公式 4)
当 $\cos \left ( 2\pi f_mt ight )$ 为 -1 时,我们将得到调制波的最小振幅。
$\Rightarrow A_\min = A_c - A_m$ (公式 5)
将公式 4 和等式 5。
$$A_\max + A_\min = A_c+A_m+A_c-A_m = 2A_c$$
$\Rightarrow A_c = \frac{A_\max + A_\min}{2}$ (等式 6)
从等式 4 中减去等式 5。
$$A_\max - A_\min = A_c + A_m - \left (A_c -A_m ight )=2A_m$$
$\Rightarrow A_m = \frac{A_\max - A_\min}{2}$ (等式7)
公式 7 与公式 6 的比率如下。
$$\frac{A_m}{A_c} = \frac{\left ( A_{max} - A_{min} ight )/2}{\left ( A_{max} + A_{min} ight )/2}$$
$\Rightarrow \mu = \frac{A_\max - A_\min}{A_\max + A_\min}$ (公式 8)
因此,公式 3 和公式 8 是调制指数的两个公式。调制指数或调制深度通常以百分比表示,称为调制百分比。我们只需将调制指数值乘以 100,即可获得调制百分比。
对于完美的调制,调制指数的值应为 1,这意味着调制百分比应为 100%。
例如,如果此值小于 1,即调制指数为 0.5,则调制输出将如下图所示。这被称为欠调制。这样的波被称为欠调制波。
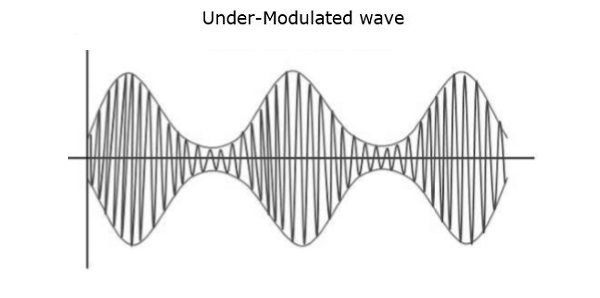
如果调制指数的值大于 1,即 1.5 左右,则该波将是过调制波。它看起来如下图所示。
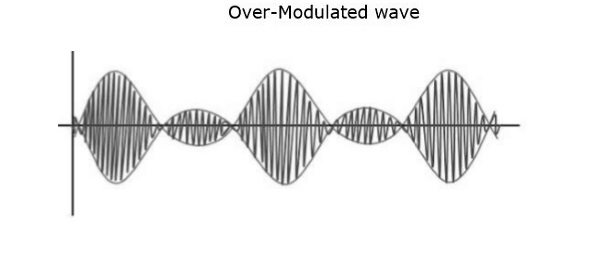
随着调制指数值的增加,载波会经历 180o 相位反转,从而导致额外的边带,因此波会失真。这种过调制波会造成干扰,而干扰是无法消除的。
AM 波的带宽
带宽 (BW) 是信号最高频率和最低频率之间的差值。从数学上讲,我们可以将其写成
$$BW = f_{max} - f_{min}$$
考虑以下幅度调制波方程。
$$s\left ( t ight ) = A_c\left [ 1 + \mu \cos \left ( 2 \pi f_m t ight ) ight ] \cos\left ( 2 \pi f_ct ight )$$
$$\Rightarrow s\left ( t ight ) = A_c\cos \left ( 2\pi f_ct ight )+ A_c\mu \cos(2\pi f_ct)\cos \left ( 2\pi f_mt ight )$$
$\Rightarrow s\left ( t ight )= A_c\cos \left ( 2\pi f_ct ight )+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c+f_m ight ) t ight ]+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c-f_m ight ) t ight ]$
因此,调幅波有三个频率。这些是载波频率$f_c$、上边带频率$f_c + f_m$和下边带频率$f_c-f_m$
这里,
$f_{max}=f_c+f_m$和$f_{min}=f_c-f_m$
在带宽公式中代入$f_{max}$和$f_{min}$值。
$$BW=f_c+f_m-\left ( f_c-f_m ight )$$
$$\Rightarrow BW=2f_m$$
因此,可以说调幅波所需的带宽是调制信号频率的两倍。
AM波的功率计算
考虑以下调幅波的方程波。
$\ s\left ( t ight )= A_c\cos \left ( 2\pi f_ct ight )+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c+f_m ight ) t ight ]+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c-f_m ight ) t ight ]$
AM波的功率等于载波、上边带和下边带频率分量功率之和。
$$P_t=P_c+P_{USB}+P_{LSB}$$
我们知道余弦信号功率的标准公式是
$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m/ \sqrt{2} ight )^2}{2}$$
其中,
$v_{rms}$是余弦信号的均方根值。
$v_m$是余弦信号的峰值。
首先,让我们逐一找到载波、上边带和下边带的功率。
载波功率
$$P_c=\frac{\left ( A_c/\sqrt{2} ight )^2}{R}=\frac{{A_{c}}^{2}}{2R}$$
上边带功率
$$P_{USB}=\frac{\left ( A_c\mu /2\sqrt{2} ight )^2}{R}=\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}$$
同样,我们将获得与上边带功率相同的下边带功率。
$$P_{LSB}=\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}$$
现在,让我们将这三个功率相加,以获得 AM 波的功率。
$$P_t=\frac{{A_{c}}^{2}}{2R}+\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}+\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}$$
$$\Rightarrow P_t=\left ( \frac{{A_{c}}^{2}}{2R} ight )\left ( 1+\frac{\mu ^2}{4}+\frac{\mu ^2}{4} ight )$$
$$\Rightarrow P_t=P_c\left ( 1+\frac{\mu ^2}{2} ight )$$
当载波功率和调制指数已知时,我们可以使用上述公式来计算AM波的功率。
如果调制指数$\mu=1$,则AM波的功率等于载波功率的1.5倍。因此,传输 AM 波所需的功率是完美调制载波功率的 1.5 倍。


