凸优化 - 线性规划

方法论

线性规划也称为线性优化，是一种用于解决关系本质上是线性的数学问题的技术。线性规划的基本性质是最大化或最小化目标函数，并受到一些约束。目标函数是从问题的数学模型中获得的线性函数。约束是强加于模型的条件，也是线性的。

• 根据给定的问题，找到目标函数。
• 找到约束。
• 在图形上绘制约束。
• 找到可行区域，它由所有约束的交点形成。
• 找到可行区域的顶点。
• 找到这些顶点处的目标函数值。
• 最大化或最小化目标函数（根据问题）的顶点就是答案。

示例

步骤 1 −最大化 $5x+3y$，但要满足

$x+y\leq 2$，

$3x+y\leq 3$，

$x\geq 0 \:and \:y\geq 0$

解决方案 −

第一步是在图表上找到可行区域。

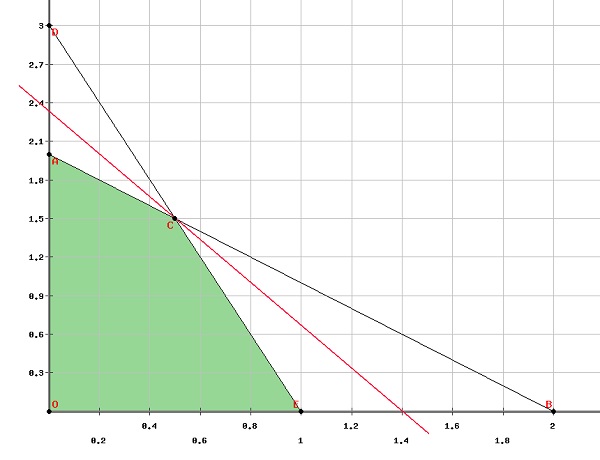
从图表中可以清楚地看出，可行区域的顶点是

$\left ( 0, 0 ight )\left ( 0, 2 ight )\left ( 1, 0 ight )\left ( \frac{1}{2}, \frac{3}{2} ight )$

设 $f\left ( x, y ight )=5x+3y$

将这些值代入目标函数，我们得到 −

$f\left ( 0, 0 ight )$=0

$f\left ( 0, 2 ight )$=6

$f\left ( 1, 0 ight )$=5

$f\left ( \frac{1}{2}, \frac{3}{2} ight )$=7

因此，函数在 $\left ( \frac{1}{2}, \frac{3}{2} ight )$ 处最大化

步骤 2 − 一家手表公司生产一款电子表和一款机械表。长期预测显示，预计每天至少需要 100 只电子表和 80 只机械表。由于产能限制，每天最多只能生产 200 只电子表和 170 只机械表。为了满足运输合同，每天至少要运送 200 块手表。

如果每售出一块电子表会造成 $\$2$ 的损失，但每块机械表会产生 $\$5$ 的利润，那么每天每种类型应该生产多少块才能使净利润最大化？

解决方案 −

设 $x$ 为生产的电子表数量

$y$ 为生产的机械表数量

根据问题，每天至少要生产 100 块电子表，最多可以生产 200 块电子表。

$\Rightarrow 100 \leq \:x\leq 200$

同样，每天至少要生产 80 块机械表，最多可以生产 170 块机械表。

$\Rightarrow 80 \leq \:y\leq 170$

由于每天至少要生产 200 块手表。

$\Rightarrow x +y\leq 200$

由于每售出一块电子表都会造成 $\$2$ 的损失，但每售出一块机械表都会产生 $\$5$ 的利润，

总利润可以计算为

$利润 =-2x + 5y$

我们必须最大化利润，因此，问题可以表述为 −

最大化 $-2x + 5y$，但要满足

$100 \:\leq x\:\leq 200$

$80 \:\leq y\:\leq 170$

$x+y\:\leq 200$

将上述方程绘制成图，我们得到，

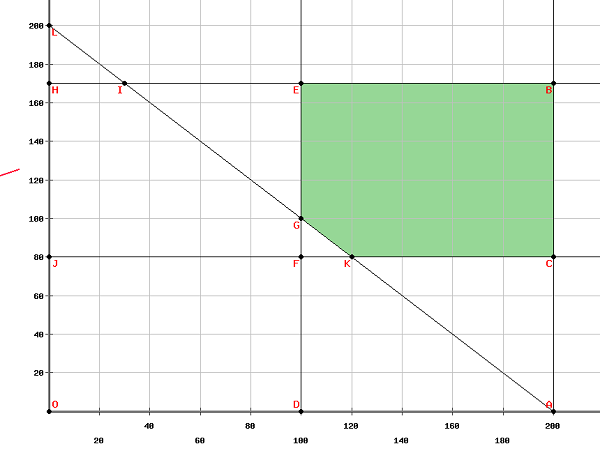
可行域的顶点为

$\left ( 100, 170 ight )\left ( 200, 170 ight )\left ( 200, 180 ight )\left ( 120, 80 ight ) 和 \left ( 100, 100 ight )$

目标函数的最大值位于 $\left ( 100, 170 ight )$ 因此，为了最大化净利润，应该生产 100 块电子表和 170 块机械表。