SciPy - integration.romb() 方法

SciPy integrate.romb() 方法用于执行数值或罗姆伯格积分任务。此方法还帮助我们根据样本/坐标点绘制图形。

语法

以下是 SciPy integrate.romb() 方法的语法 −

romb(y, dx = int_val/float_val/1.0)

参数

此函数接受以下参数 −

y:此参数确定以离散点为值的数组函数，这些点考虑偶数间距。
dx:此参数确定点之间的间距，如果未指定，则默认值为 1.0。

返回值

此方法返回浮点类型的估计值。

示例 1

以下是 SciPy integrate.romb() 方法，它显示了在 0 和 1 之间的区间内简单的积分函数 f(x) = x²。基于五个离散点的结果值。

import numpy as np
from scipy import integration

# 定义离散点处的函数值
x = np.linspace(0, 1, 5)
y = x**2

# 计算积分
res_integral = integration.romb(y, dx=x[1] - x[0])

# 显示结果
print(res_integral)

输出

上述代码产生以下结果 −

0.3333333333333333

示例 2

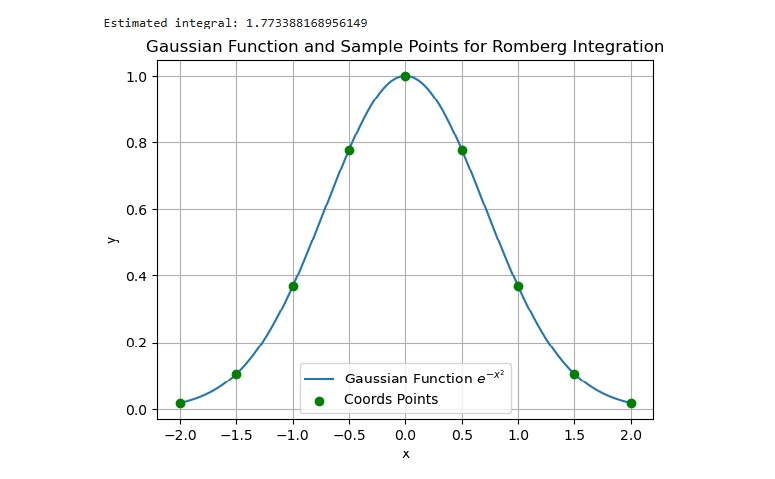
此程序演示了高斯函数 e^-x² 在 -2 到 2 之间的区间上的数值积分，函数值表示为九个点(x 轴)。

import numpy as np
from scipy.integrate import romb
import matplotlib.pyplot as plt

# 定义离散点处的函数值
x = np.linspace(-2, 2, 9)
y = np.exp(-x**2)

# 计算积分
res_integral = romb(y, dx=x[1] - x[0])

# 显示结果
print(f"估计积分:{res_integral}")

# 绘制高斯函数和 Romberg 积分中使用的点
x_fine = np.linspace(-2, 2, 1000)
y_fine = np.exp(-x_fine**2)

plt.plot(x_fine, y_fine, label='Gaussian Function $e^{-x^2}$')
plt.scatter(x, y, color='green', zorder=5, label='coords Points')

plt.title('Gaussian Function and Sample Points for Romberg Integration')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()