SciPy - linkage() 方法
SciPy linkage() 方法适用于层次聚类,可用于执行链接矩阵的任务。此矩阵提供矩阵数据的代码结构。
层次聚类是通过将数据分成基于组的组来定义的。以下是数据分析中的两种用途 −
- 识别自然分组:它用于借助自然划分来识别分组项。
- 树状图构建:这将创建一个树状图,它是一种记录数据分割序列或层次结构的树形图。
此方法通常用于数据分析,将相似的项目分组为簇,这可以帮助我们理解数据的结构并进行预测。
语法
以下是 SciPy linkage() 方法的语法 −
linkage(data, method = 'single') 或, linkage(data, method = 'single', metric = 'type')
参数
此方法接受以下参数 −
- data:此参数以数组形式定义数据元素列表。
- method = 'single':此参数定义链接算法的类型。
- metric = 'type':默认类型为"euclidean"。
返回值
此方法返回链接矩阵,其形状为 numpy 数组(n-1, 4),其中 n 定义观察次数。
示例 1
以下是 SciPy linkage() 方法对链接聚类进行操作自定义数据集并绘制树状图以可视化数据聚类过程。
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
# 样本数据
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8]])
# 使用单链接计算链接矩阵
result = linkage(data, method='single')
# 绘制树状图
plt.figure(figsize=(8, 4))
dendrogram(result)
plt.title('Dendrogram - Single Linkage')
plt.xlabel('Sample index')
plt.ylabel('Distance')
plt.show()
输出
上述代码产生以下结果 −
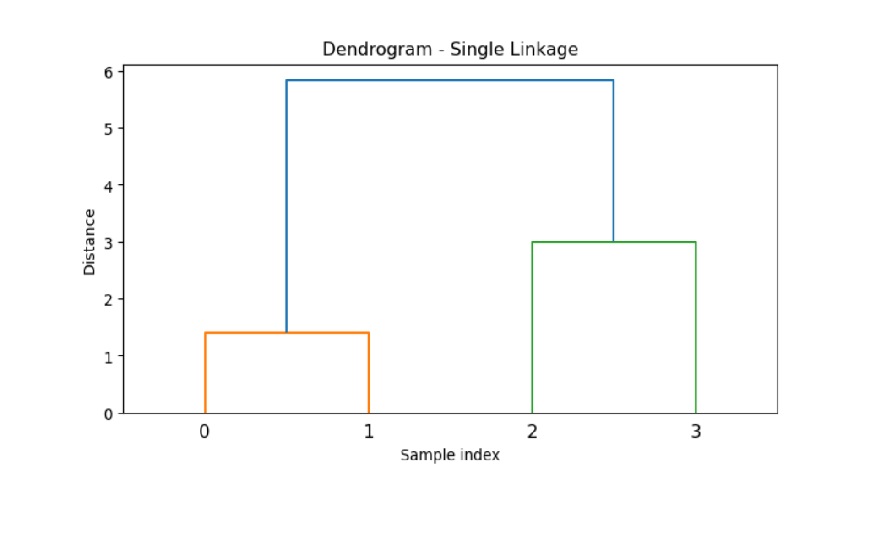
示例 2
在这里,我们演示了对具有六个观测值的数据集进行完整的链接聚类,并使用欧几里得距离度量绘制了树状图。
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
# 样本数据
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [2, 1]])
# 使用完整链接和欧几里得距离计算链接矩阵
result = linkage(data, method='complete', metric='euclidean')
# 绘制树状图
plt.figure(figsize=(8, 4))
dendrogram(result)
plt.title('Dendrogram - Complete Linkage')
plt.xlabel('Sample index')
plt.ylabel('Distance')
plt.show()
输出
上述代码产生以下结果 −
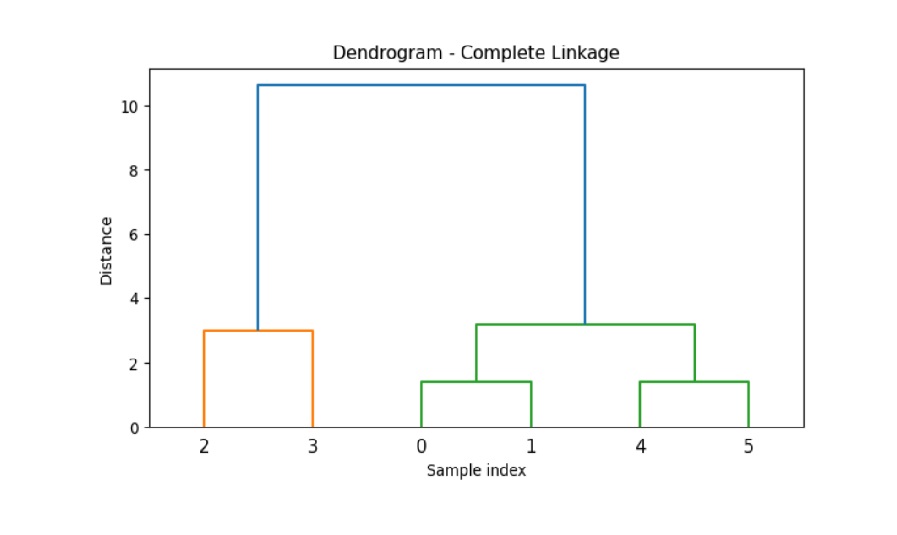
示例 3
以下示例执行平均使用曼哈顿距离对与示例 2 相同的数据集进行链接聚类。此处,它使用度量类型作为"城市街区"。
请注意,曼哈顿距离是使用直角的两个点轴来测量的。它用于高维数据集。
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
# 样本数据
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [2, 1]])
# 使用平均链接和曼哈顿距离计算链接矩阵
result = linkage(data, method='average', metric='cityblock')
# 绘制树状图
plt.figure(figsize=(8, 4))
dendrogram(result)
plt.title('树状图 - 具有曼哈顿距离的平均链接')
plt.xlabel('样本索引')
plt.ylabel('距离')
plt.show()
输出
上述代码产生以下结果 −
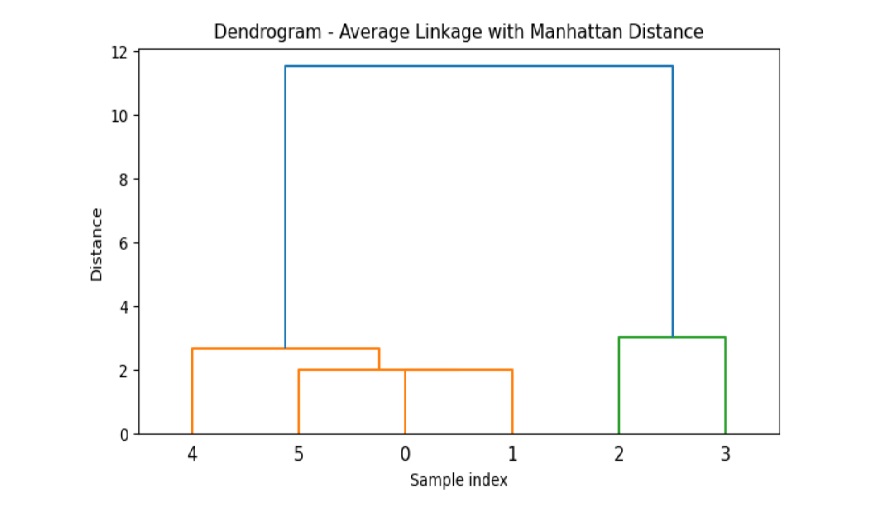
 scipy_reference.html
scipy_reference.html
