MATLAB - 多项式

MATLAB 将多项式表示为包含按降幂排序的系数的行向量。 例如，方程 P(x) = x⁴ + 7x³ - 5x + 9 可以表示为 −

p = [1 7 0 -5 9];

计算多项式

polyval 函数用于计算指定值处的多项式。 例如，要计算之前的多项式 p，在 x = 4 处，请输入 −

p = [1 7 0  -5 9];
polyval(p,4)

MATLAB 执行上述语句并返回以下结果 −

ans = 693

MATLAB 还提供了 polyvalm 函数来计算矩阵多项式。 矩阵多项式是以矩阵为变量的多项式。

例如，让我们创建一个方阵 X 并计算 X 处的多项式 p −

p = [1 7 0  -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)

MATLAB 执行上述语句并返回以下结果 −

ans =
      2307       -1769        -939        4499
      2314       -2376        -249        4695
      2256       -1892        -549        4310
      4570       -4532       -1062        9269

求多项式的根

roots 函数计算多项式的根。 例如，要计算多项式 p 的根，请输入 −

p = [1 7 0  -5 9];
r = roots(p)

MATLAB 执行上述语句并返回以下结果 −

r =
   -6.8661 + 0.0000i
   -1.4247 + 0.0000i
   0.6454 + 0.7095i
   0.6454 - 0.7095i

函数poly是根函数的反函数，返回多项式系数。 例如 −

p2 = poly(r)

MATLAB 执行上述语句并返回以下结果 −

p2 =

   Columns 1 through 3:

      1.00000 + 0.00000i   7.00000 + 0.00000i   0.00000 + 0.00000i

   Columns 4 and 5:

      -5.00000 - 0.00000i   9.00000 + 0.00000i

多项式曲线拟合

polyfit 函数查找以最小二乘意义拟合一组数据的多项式的系数。 如果 x 和 y 是两个向量，其中包含要拟合到 n 次多项式的 x 和 y 数据，那么我们可以通过以下方式获得拟合数据的多项式 −

p = polyfit(x,y,n)

示例

创建脚本文件并输入以下代码 −

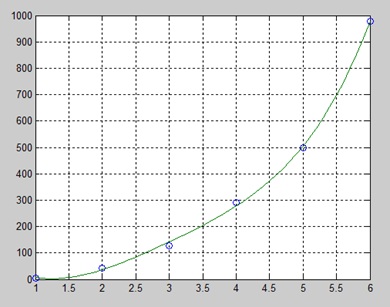
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67];   %data
p = polyfit(x,y,4)   %get the polynomial

% 计算更精细范围内的 polyfit 估计值，
% 并根据实际数据值绘制估计值以进行比较:
x2 = 1:.1:6;          
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on

运行该文件时，MATLAB 显示以下结果 −

p =
   4.1056  -47.9607  222.2598 -362.7453  191.1250

并绘制下图 −