Mahotas - 小波变换
小波变换是一种数学技术,用于将图像分解为不同的频率分量。小波变换可捕获图像的局部和全局细节。
小波变换使用称为小波的小波形函数来分析信号。这些小波经过缩放和变换以匹配图像中存在的不同模式。
小波变换涉及修改频率分量的高频和低频系数以产生识别模式并增强图像。可以通过逆小波变换恢复原始图像。
让我们讨论小波变换技术及其逆变换。
Daubechies 变换
Daubechies 变换是一种小波变换技术,用于将信号分解为不同的频率分量。它使我们能够在时域和频域中分析信号。
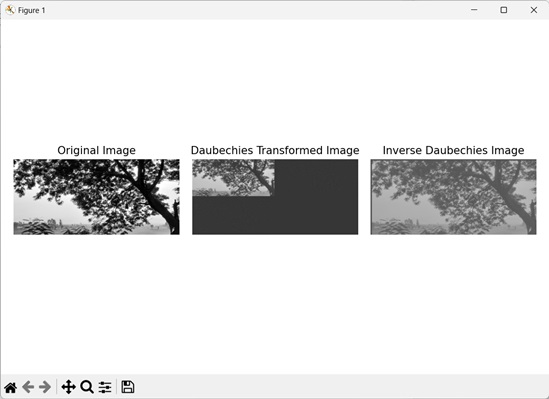
让我们看看下面的 Daubechies 变换图像 −

逆 Daubechies 变换
逆 Daubechies 变换是 Daubechies 变换的逆过程。它从通过 Daubechies 变换获得的各个频率分量重建原始图像。
通过应用逆变换,我们可以恢复信号同时保留重要细节。
在这里,我们看一下 Daubechies 变换的逆 −
Haar 变换
Haar 变换技术通过将图像划分为子区域,将其分解为不同的频率分量。然后计算平均值之间的差异以对图像应用小波变换。
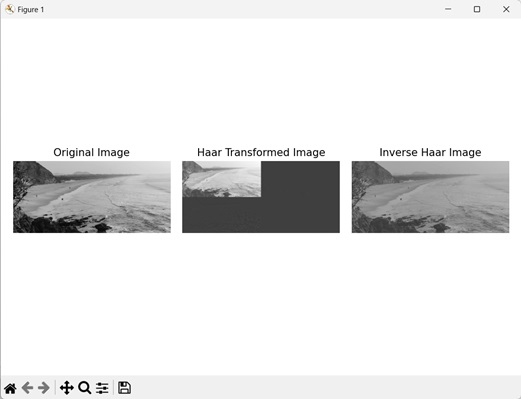
在下图中,我们看到了 Haar 变换后的图像 −

逆 Haar
逆 Haar 变换根据通过 Haar 变换获得的频率分量重建原始图像。它是 Haar 变换的逆操作。
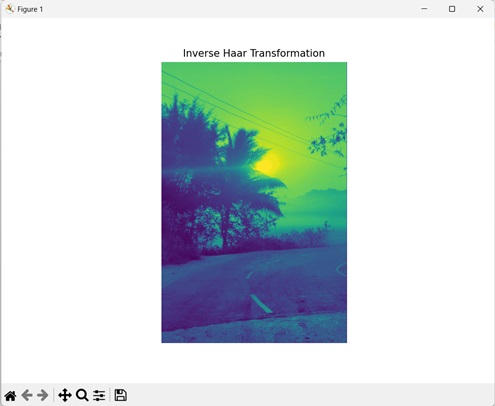
让我们看看 Haar 变换的逆 −
示例
在下面的例子中,我们尝试执行上面解释的所有小波变换 −
import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
image = mh.imread('sun.png', as_grey=True)
# Daubechies 变换
daubechies = mh.daubechies(image, 'D6')
mtplt.imshow(daubechies)
mtplt.title('Daubechies Transformation')
mtplt.axis('off')
mtplt.show()
# 逆 Daubechies 变换
daubechies = mh.daubechies(image, 'D6')
inverse_daubechies = mh.idaubechies(daubechies, 'D6')
mtplt.imshow(inverse_daubechies)
mtplt.title('Inverse Daubechies Transformation')
mtplt.axis('off')
mtplt.show()
# 哈尔变换
haar = mh.haar(image)
mtplt.imshow(haar)
mtplt.title('Haar Transformation')
mtplt.axis('off')
mtplt.show()
# 逆哈尔变换
haar = mh.haar(image)
inverse_haar = mh.ihaar(haar)
mtplt.imshow(inverse_haar)
mtplt.title('Inverse Haar Transformation')
mtplt.axis('off')
mtplt.show()
输出
得到的输出如下所示 −
Daubechies 变换:
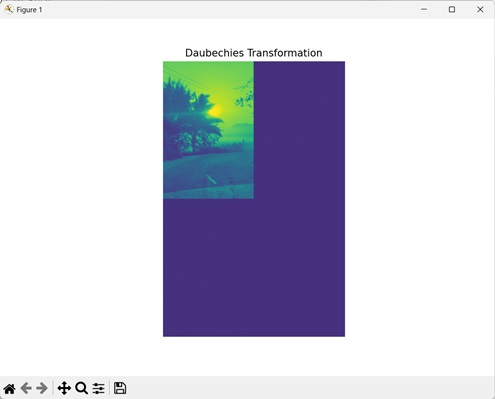
Daubechies 逆变换:
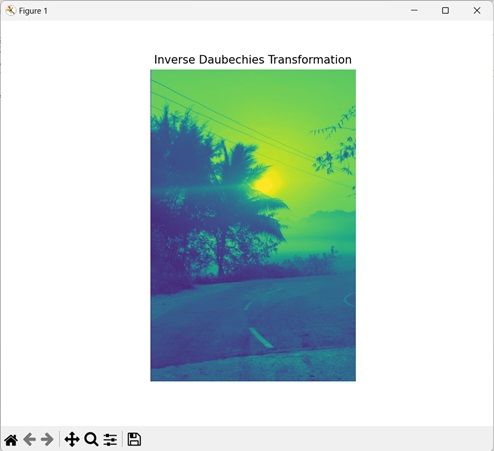
Haar 变换:

Haar 逆变换:
我们将在其余章节。


