Mahotas - 高斯滤波

高斯滤波是一种用于模糊或平滑图像的技术。它可以减少图像中的噪声并柔化锐利的边缘。

想象一下您的图像是一个由微小点组成的网格，每个点代表一个像素。高斯滤波的工作原理是获取每个像素并根据周围像素调整其值。

它计算其邻域内像素值的加权平均值，将更多重点放在较近的像素上，而较少重点放在较远的像素上。

通过对图像中的每个像素重复此过程，高斯滤波器通过平滑不同区域之间的急剧过渡并降低噪声来模糊图像。

滤波器的大小决定了模糊的程度。过滤器尺寸越大，考虑的区域越广，模糊效果就越明显。

简单来说，高斯滤波通过平均附近的像素值使图像看起来更平滑，更重视较近的像素，而较远的像素则不那么重要。这有助于减少噪音，使图像不那么清晰。

Mahotas 中的高斯滤波

在 Mahotas 中，我们可以使用 mahotas.gaussian_filter() 函数对图像执行高斯滤波。此函数使用称为高斯核的特殊矩阵对图像应用模糊效果。

高斯核是一种特殊的矩阵，其数字以特定方式排列。核中的每个数字代表一个权重。

将内核放置在图像中的每个像素上，并将相邻像素的值乘以内核中相应的权重。

然后将相乘的值相加，并将其作为新值分配给中心像素。对图像中的每个像素重复此过程，从而产生模糊图像，其中清晰的细节和噪声减少。

mahotas.gaussian_filter() 函数

mahotas.gaussian_filter() 函数将灰度图像作为输入，并返回模糊版本的图像作为输出。

模糊量由 sigma 值决定。sigma 值越高，应用于输出图像的模糊程度就越大。

语法

以下是 mahotas &minus 中 gaussian_filter() 函数的基本语法;

mahotas.gaussian_filter(array, sigma, order=0, mode='reflect', cval=0.,
out={np.empty_like(array)})

其中，

• array − 为输入图像。

• sigma − 确定高斯核的标准差。

• order (可选) − 指定高斯滤波器的阶数。其值可以是 0、1、2 或 3(默认为 0)。

• mode (可选) −它指定应如何处理边框(默认为"反射")。

• cval(可选) − 它表示模式为"常量"时应用的填充值(默认为 0)。

• out(可选) − 它指定存储输出图像的位置(默认为与数组大小相同的数组)。

示例

在下面的示例中，我们使用 mh.gaussian_filter() 函数对图像应用高斯滤波。

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
# 加载图像
image = mh.imread('tree.tiff')
# 将其转换为灰度
image = mh.colors.rgb2gray(image)
# 应用高斯滤波
gauss_filter = mh.gaussian_filter(image, 4)
# 为子图创建图形和轴
fig, axis = mtplt.subplots(1, 2)
# 显示原始图像
axes[0].imshow(image)
axes[0].set_title('Original Image')
axes[0].set_axis_off()
# 显示高斯滤波图像
axes[1].imshow(gauss_filter)
axes[1].set_title('Gaussian Filtered Image')
axes[1].set_axis_off()
# 调整子图之间的间距
mtplt.tight_layout()
# 显示图
mtplt.show()

输出

以下是上述代码的输出 −

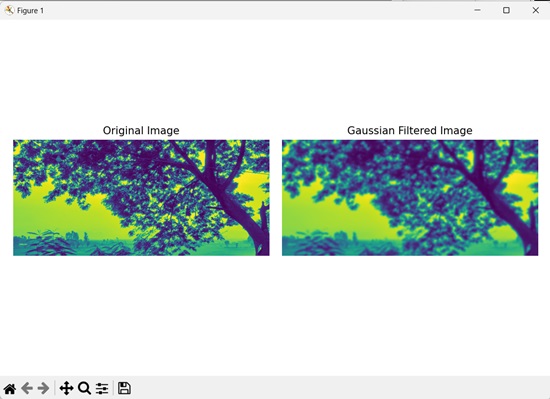
使用不同阶数进行滤波

我们可以对具有不同阶数的图像执行高斯滤波。高斯滤波中的阶数决定了应用于图像的平滑度(模糊度)。

阶数值越高，应用于图像的平滑效果就越强。

在处理噪声很大的图像时，阶数越高很有用。但是，由于滤波器应用多次，阶数越高也会增加处理时间。

阶数为 0 时应用高斯滤波器一次，阶数为 1、2 或 3 时分别应用高斯滤波器两次、三次和四次。

在 mahotas 中，要执行不同阶数的高斯滤波，我们将 0 以外的任何值作为 order 参数传递给 gaussian_filter() 函数。

示例

在下面提到的示例中，我们以不同的阶数对图像应用高斯滤波。

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
# 加载图像
image = mh.imread('sea.bmp')
# 将其转换为灰度
image = mh.colors.rgb2gray(image)
# 应用高斯滤波
gauss_filter = mh.gaussian_filter(image, 3, 1)
# 为子图创建图形和轴
fig, axis = mtplt.subplots(1, 2)
# 显示原始图像
axes[0].imshow(image)
axes[0].set_title('Original Image')
axes[0].set_axis_off()
# 显示高斯滤波图像
axes[1].imshow(gauss_filter)
axes[1].set_title('Gaussian Filtered Image')
axes[1].set_axis_off()
# 调整子图之间的间距
mtplt.tight_layout()
# 显示图
mtplt.show()

输出

上述代码的输出如下 −

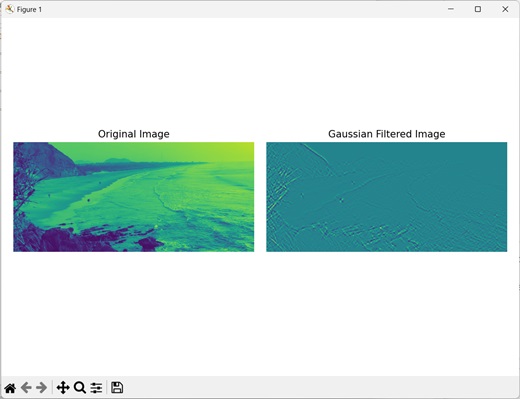
使用"镜像"模式进行过滤

将滤镜应用于图像时，确定如何处理图像的边界非常重要。镜像模式是一种常见的方法，它通过在边界处镜像图像内容来处理边界像素。

这意味着通过镜像图像内最近的像素来获得图像边界以外的值。这是通过沿边缘镜像现有像素来实现的。

这种镜像技术可确保实际图像和镜像图像之间的平滑过渡，从而实现更好的连续性。

示例

在这里，我们在具有"镜像"模式的图像上应用高斯滤波。

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
# 加载图像
image = mh.imread('sun.png')
# 将其转换为灰度
image = mh.colors.rgb2gray(image)
# 应用高斯滤波
gauss_filter = mh.gaussian_filter(image, 3, 0, mode='mirror')
# 为子图创建图形和轴
fig, axis = mtplt.subplots(1, 2)
# 显示原始图像
axes[0].imshow(image)
axes[0].set_title('Original Image')
axes[0].set_axis_off()
# 显示高斯滤波图像
axes[1].imshow(gauss_filter)
axes[1].set_title('Gaussian Filtered Image')
axes[1].set_axis_off()
# 调整间距子图
mtplt.tight_layout()
# 显示图形
mtplt.show()

输出

执行上述代码后，我们得到以下输出 −