Mahotas - 图像的偏心率

图像的偏心率是指图像中物体或区域形状的拉长程度。它定量衡量了形状与完美圆形的偏差程度。

偏心率值介于 0 和 1 之间，其中 −

• 0 − 表示完美圆形。偏心率为 0 的物体伸长率最小，并且完全对称。

• 接近 1 − 表示形状越来越拉长。当偏心率值接近 1 时，形状会变得更细长，不再是圆形。

Mahotas 中图像的偏心率

我们可以使用 'mahotas.features.eccentricity()' 函数计算 Mahotas 中图像的偏心率。

如果偏心率值较高，则表示图像中的形状拉伸或拉长较多。另一方面，如果偏心率值较低，则表示形状更接近完美的圆形或拉长较少。

mahotas.features.eccentricity() 函数

mahotas 中的 eccentricity() 函数可帮助我们测量图像中形状的拉伸或拉长程度。此函数以单通道图像作为输入，并返回 0 到 1 之间的浮点数。

语法

以下是 mahotas − 中 eccentricity() 函数的基本语法

mahotas.features.eccentricity(bwimage)

其中，'bwimage' 是解释为布尔值的输入图像。

示例

在下面的示例中，我们正在寻找图像的偏心率 −

import mahotas as mh
import numpy as np
from pylab import imshow, show
image = mh.imread('nature.jpeg', as_grey = True)
eccentricity= mh.features.eccentricity(image)
print("图像偏心率 =", eccentricity)

输出

上述代码的输出如下 −

图像偏心率 = 0.8902515127811386

使用二值图像计算偏心率

要将灰度图像转换为二值格式，我们使用一种称为阈值的技术。此过程有助于我们将图像分成两部分 − 前景(白色)和背景(黑色)。

我们通过选择一个阈值(表示像素强度)来实现这一点，该阈值充当截止点。

Mahotas 通过提供">"运算符为我们简化了此过程，该运算符允许我们将像素值与阈值进行比较并创建二值图像。准备好二值图像后，我们现在可以计算偏心率了。

示例

在这里，我们尝试计算二值图像的偏心率 −

import mahotas as mh
image = mh.imread('nature.jpeg', as_grey=True)
# 根据固定阈值将图像转换为二值
threshold = 128
binary_image = image > 阈值
# 计算偏心率
eccentricity = mh.features.eccentricity(binary_image)
print("偏心率:", eccentricity)

输出

执行上述代码后，我们得到以下输出 −

偏心率:0.7943319646935899

使用骨架化计算偏心率

骨架化，也称为细化，是一种旨在减少物体形状或结构的过程，将其表示为细骨架。我们可以使用 mahotas 中的 thin() 函数实现此目的。

mahotas.thin() 函数以二进制图像作为输入，其中感兴趣的对象由白色像素(像素值为 1)表示，背景由黑色像素(像素值为 0)表示。

我们可以使用骨架化通过将图像简化为其骨架表示来计算图像的偏心率。

示例

现在，我们正在使用骨架化计算图像的偏心率 −

import mahotas as mh
import matplotlib.pyplot as plt
# 读取图像并将其转换为灰度
image = mh.imread('tree.tiff')
grey_image = mh.colors.rgb2grey(image)
# 对图像进行骨架化
skeleton = mh.thin(grey_image)
# 计算骨架化图像的偏心率
eccentricity = mh.features.eccentricity(skeleton)
# 打印偏心率
print(eccentricity)
# 创建带有子图的图形
fig, axis = plt.subplots(1, 2, figsize=(7,5 ))
# 显示原始图像
axes[0].imshow(image)
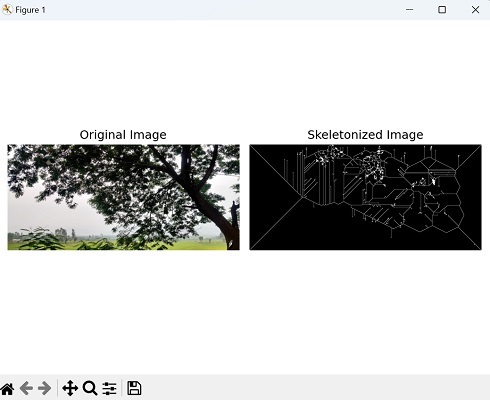
axes[0].set_title('Original Image')
axes[0].axis('off')
# 显示骨架化图像
axes[1].imshow(skeleton, cmap='gray')
axes[1].set_title('Skeletonized Image')
axes[1].axis('off')
# 调整布局并显示图
plt.tight_layout()
plt.show()

输出

得到的输出如下图所示 −

0.8975030064719701

显示的图像如下图所示 −