Mahotas - 图像卷积

图像处理中的卷积用于对图像执行各种过滤操作。

以下是其中一些 −

• 提取特征 − 它用于通过应用特定过滤器来检测边缘、角落、斑点等特征。

• 过滤 − 它用于对图像执行平滑和锐化操作。

• 压缩 − 我们可以通过删除图像中的冗余信息来压缩图像。

Mahotas 中的图像卷积

在 Mahotas 中，您可以使用 convolve() 函数对图像执行卷积。此函数接受两个参数−输入图像和内核;其中，内核是一个小矩阵，它定义卷积期间要应用的操作，例如模糊、锐化、边缘检测或任何其他所需效果。

使用 convolve() 函数

convolve() 函数用于对图像执行卷积。卷积是一种数学运算，它采用两个数组 - 图像和卷积核，并生成第三个数组(输出图像)。

卷积核是一个小数字数组，用于过滤图像。卷积运算通过将图像和内核的相应元素相乘，然后将结果相加来执行。卷积操作的输出是经过内核过滤的新图像。

以下语法在 mahotas − 中执行卷积

convolve(image, kernel, mode='reflect', cval=0.0, out=None)

其中，

• image − 是输入图像。

• kernel − 是卷积内核。

• mode − 指定如何处理图像的边缘。它可以是反射、最近常数、忽略、包裹或镜像。默认选择 Reflect。

• cval − 它指定用于图像外部像素的值。

• out − 它指定输出图像。如果未指定 out 参数，则将创建一个新图像。

示例

在下面的示例中，我们首先使用 mh.imresize() 函数将输入图像"nature.jpeg"的大小调整为"4×4"形状。然后，我们创建一个"4×4"内核，所有值都设置为 1。最后，我们使用 mh.convolve() 函数执行卷积−

import mahotas as mh
import numpy as np
# 加载图像
image = mh.imread('nature.jpeg', as_grey=True)
# 将图像大小调整为 4x4
image = mh.imresize(image, (4, 4))
# 创建 4x4 内核
kernel = np.ones((4, 4))
# 执行卷积
result = mh.convolve(image, kernel)
print (result)

输出

以下是上述代码的输出 −

[[3155.28 3152.84 2383.42 1614. ]
[2695.96 2783.18 2088.38 1393.58]
[1888.48 1970.62 1469.53 968.44]
[1081. 1158.06 850.68 543.3 ]]

使用高斯核进行卷积

Mahotas 中的高斯核是一个小型数字矩阵，用于模糊或平滑图像。

高斯核对每个像素应用加权平均值，其中权重由称为高斯分布的钟形曲线确定。核为附近的像素赋予较高的权重，为远处的像素赋予较低的权重。此过程有助于减少噪音并增强图像中的特征，从而产生更平滑、更美观的输出。

以下是 mahotas − 中高斯核的基本语法

mahotas.gaussian_filter(array, sigma)

其中，

• array − 它是输入数组。

• sigma − 它是高斯核的标准差。

示例

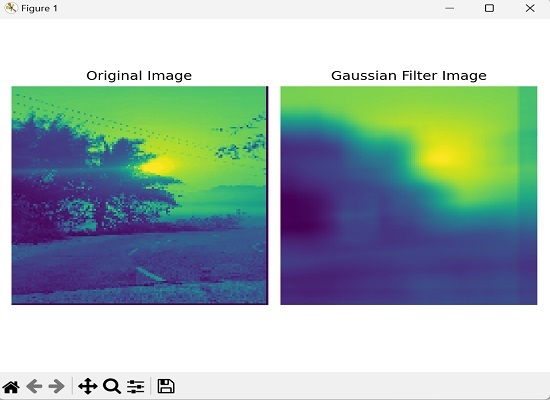
以下是使用高斯滤波器对图像进行卷积的示例。在这里，我们调整图像大小，将其转换为灰度，应用高斯滤波器模糊图像，然后并排显示原始图像和模糊图像 −

import mahotas as mh
import matplotlib.pyplot as mtplt
# 加载图像
image = mh.imread('sun.png')
# 如果需要，转换为灰度
if len(image.shape) > 2:
   image = mh.colors.rgb2gray(image)
# 将图像大小调整为 128x128
image = mh.imresize(image, (128, 128))
# 创建高斯核
kernel = mh.gaussian_filter(image, 1.0)
# 将核的大小减小为 20x20
kernel = kernel[:20, :20]
# 模糊图像
blurred_image = mh.convolve(image, kernel)
# 创建图形和子图
fig, axis = mtplt.subplots(1, 2)
# 显示原始图像
axes[0].imshow(image)
axes[0].axis('off')
axes[0].set_title('Original Image')
# 显示模糊图像
axes[1].imshow(blurred_image)
axes[1].axis('off')
axes[1].set_title('Gaussian Filter Image')
# 调整间距和布局
mtplt.tight_layout()
# 显示图形
mtplt.show()

输出

上述代码的输出如下 −

带填充的卷积

Mahotas 中的带填充的卷积是指在执行卷积操作之前在图像边缘周围添加额外的像素或边框。填充的目的是创建一个尺寸增加的新图像，而不会丢失原始图像边缘的信息。

填充确保内核可以应用于所有像素，包括边缘像素，从而产生与原始图像大小相同的卷积输出。

示例

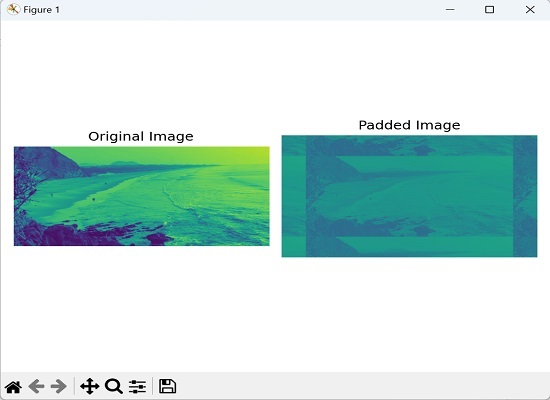
在这里，我们将自定义内核定义为 NumPy 数组，以强调图像的边缘 −

import numpy as np
import mahotas as mh
import matplotlib.pyplot as mtplt
# 创建自定义内核
kernel = np.array([[0, -1, 0],[-1, 5, -1],
[0, -1, 0]])
# 加载图像
image = mh.imread('sea.bmp', as_grey=True)
# 为图像添加填充
padding = np.pad(image, 150, mode='wrap')
# 使用填充执行卷积
padded_image = mh.convolve(padding, kernel)
# 创建图形和子图
fig, axis = mtplt.subplots(1, 2)
# 显示原始图像
axes[0].imshow(image)
axes[0].axis('off')
axes[0].set_title('Original Image')
# 显示填充图像
axes[1].imshow(padded_image)
axes[1].axis('off')
axes[1].set_title('Padded Image')
# 调整间距和布局
mtplt.tight_layout()
# 显示图像
mtplt.show()

输出

执行上述代码后，我们得到以下输出 −

使用盒式过滤器进行卷积以实现模糊效果

Mahotas 中的盒式过滤器卷积是一种可用于模糊图像的技术。盒式过滤器是一种简单的过滤器，其中过滤器内核中的每个元素都具有相同的值，从而产生均匀的权重分布。

使用盒式过滤器进行卷积涉及在图像上滑动内核并取内核覆盖区域中像素值的平均值。然后使用该平均值替换输出图像中的中心像素值。

对图像中的所有像素重复该过程，从而产生原始图像的模糊版本。模糊量由内核的大小决定，内核越大，模糊度越高。

示例

以下是使用框式过滤器执行卷积以模糊图像的示例 −

import mahotas as mh
import numpy as np
import matplotlib.pyplot as plt
# 加载图像
image = mh.imread('sun.png', as_grey=True)
# 定义框式过滤器的大小
box_size = 25
# 创建框式过滤器
box_filter = np.ones((box_size, box_size)) / (box_size * box_size)
# 使用框式过滤器执行卷积
blurred_image = mh.convolve(image, box_filter)
# 显示原始图像和模糊图像
fig, axis = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')
axes[1].imshow(blurred_image, cmap='gray')
axes[1].set_title('Blurred Image')
axes[1].axis('off')
plt.show()

输出

我们得到如下所示的输出 −

使用 Sobel 滤波器进行卷积以进行边缘检测

Sobel 滤波器通常用于边缘检测。它由两个独立的滤波器组成−一个用于检测水平边缘，另一个用于检测垂直边缘。

通过将 Sobel 滤波器与图像进行卷积，我们获得一张新图像，其中边缘突出显示，而图像的其余部分则显得模糊。突出显示的边缘通常比周围区域具有更高的强度值。

示例

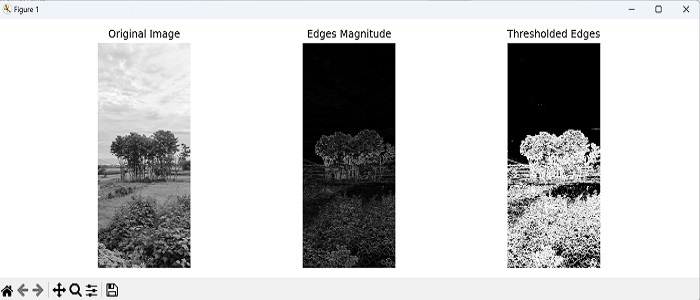
在这里，我们使用 Sobel 滤波器通过将它们与灰度图像进行卷积来执行边缘检测。然后，我们计算边缘的大小并应用阈值以获得检测到的边缘的二值图像 −

import mahotas as mh
import numpy as np
import matplotlib.pyplot as plt
image = mh.imread('nature.jpeg', as_grey=True)
# 对水平边缘应用 Sobel 滤波器
sobel_horizo​​ntal = np.array([[1, 2, 1],
[0, 0, 0],[-1, -2, -1]])
# 使用滤波器核对图像进行卷积
edges_horizo​​ntal = mh.convolve(image, sobel_horizo​​ntal)
# 对垂直边缘应用 Sobel 滤波器
sobel_vertical = np.array([[1, 0, -1],[2, 0, -2],[1, 0, -1]])
# 使用滤波器核对图像进行卷积
edges_vertical = mh.convolve(image, sobel_vertical)
# 计算边缘的大小
edges_magnitude = np.sqrt(edges_horizo​​ntal**2 + edge_vertical**2)
# 对边缘进行阈值处理
threshold = 50
thresholded_edges = edge_magnitude > Threshold
# 显示原始图像和检测到的边缘
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')
axes[1].imshow(edges_magnitude, cmap='gray')
axes[1].set_title('Edges Magnitude')
axes[1].axis('off')
axes[2].imshow(thresholded_edges, cmap='gray')
axes[2].set_title('Thresholded Edges')
axes[2].axis('off')
plt.tight_layout()
plt.show()

输出

获得的输出如下 −