布尔代数

布尔代数用于分析和简化数字（逻辑）电路。它仅使用二进制数，即 0 和 1。它也被称为二进制代数或逻辑代数。布尔代数由乔治·布尔于 1854 年发明。

布尔代数中的规则

以下是布尔代数中使用的重要规则。

• 使用的变量只能有两个值。二进制 1 表示高，二进制 0 表示低。

• 变量的补码用上划线 (-) 表示。因此，变量 B 的补码表示为 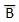。因此，如果 B = 0，则 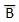= 1，如果 B = 1，则 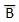= 0。

• 变量的"或"运算用它们之间的加号 (+) 表示。例如，A、B、C 的"或"运算表示为 A + B + C。

• 两个或多个变量的逻辑"与"运算用它们之间写一个点表示，例如 A.B.C。有时可以像 ABC 一样省略点。

布尔定律

布尔定律有六种类型。

交换律

任何满足以下表达式的二元运算都称为交换运算。

交换律指出，改变变量的顺序不会对逻辑电路的输出产生任何影响。

结合律

该定律指出，逻辑运算的执行顺序无关紧要，因为它们的效果是相同的。

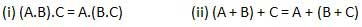
分配律定律

分配律陈述了以下条件。

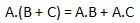
与律

这些定律使用与运算。因此，它们被称为与定律。

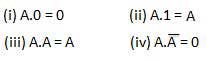
或律

这些定律使用或运算。因此，它们被称为或定律。

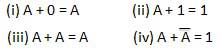
逆律

此定律使用非运算。反转定律指出，变量的双重反转将导致原始变量本身。

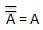
重要的布尔定理

以下是一些重要的布尔定理。