组合电路
组合电路是一种将电路中的不同门组合在一起的电路,例如编码器、解码器、多路复用器和多路分解器。组合电路的一些特性如下 −
组合电路在任何时刻的输出仅取决于输入端的电平。
组合电路不使用任何内存。输入的先前状态对电路的当前状态没有任何影响。
组合电路可以有 n 个输入和 m 个输出。
框图
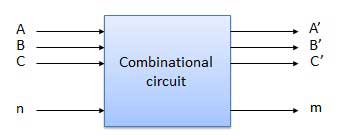
我们将详细说明几个重要的组合电路。
半加器
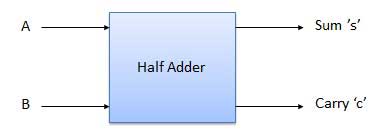
半加器是一个具有两个输入和两个输出的组合逻辑电路。半加器电路用于将两个单比特二进制数 A 和 B 相加。它是两个单比特数相加的基本构建块。该电路有两个输出进位和和。
框图
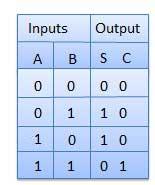
真值表
电路图
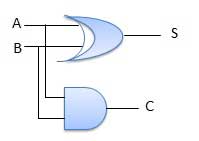
全加器
全加器是为了克服半加器电路的缺点而开发的。它可以将两个一位数 A 和 B 相加,并进位 c。全加器是一个三输入和两输出的组合电路。
框图
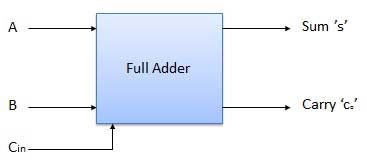
真值表
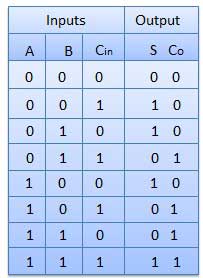
电路图
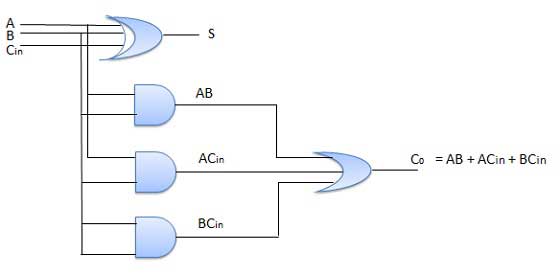
N 位并行加法器
全加器只能将两个单数二进制数和一个进位输入相加。但在实际中,我们需要添加比一位长得多的二进制数。要将两个 n 位二进制数相加,我们需要使用 n 位并行加法器。它使用多个级联的全加器。前一个全加器的进位输出连接到下一个全加器的进位输入。
4 位并行加法器
在框图中,A0 和 B0 表示四位字 A 和 B 的 LSB。因此,全加器-0 是最低级。因此,其 Cin 已永久设为 0。其余连接与图中所示的 n 位并行加法器完全相同。四位并行加法器是一种非常常见的逻辑电路。
框图
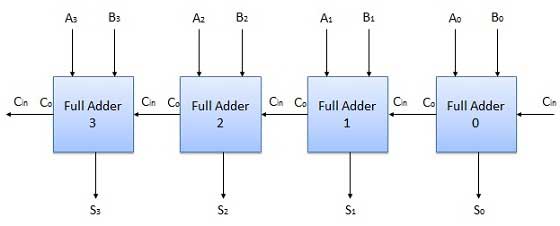
N 位并行减法器
减法可以通过取要减去的数的 1 或 2 的补码来执行。例如,我们可以通过将 B 的 1 或 2 的补码添加到 A 来执行减法 (A-B)。这意味着我们可以使用二进制加法器执行二进制减法。
4 位并行减法器
要减去的数 (B) 首先通过反相器以获得其 1 的补码。然后,4 位加法器将 A 和 B 的 2 的补码相加以进行减法。 S3 S2 S1 S0 表示二进制减法 (A-B) 的结果,进位输出 Cout 表示结果的极性。如果 A > B,则 Cout = 0,二进制形式的结果 (A-B) 则 Cout = 1,结果为 2 的补码形式。
框图
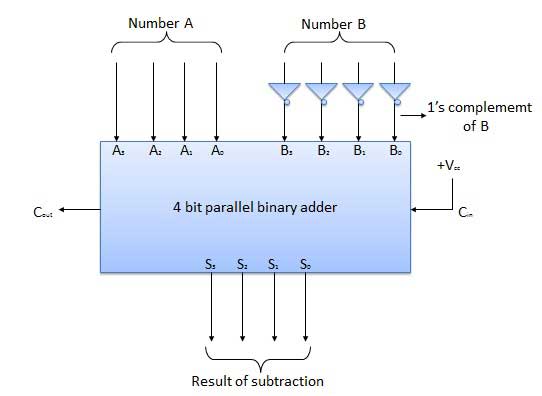
半减法器
半减法器是一个具有两个输入和两个输出(差和借位)的组合电路。它产生输入端两个二进制位之间的差,并产生一个输出(借位)以指示是否借入了 1。在减法 (A-B) 中,A 称为被减数位,B 称为减数位。
真值表
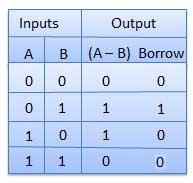
电路图
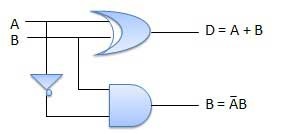
全减法器
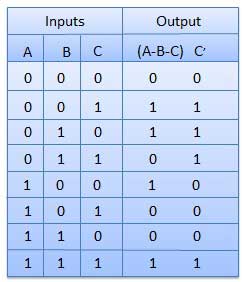
半减法器的缺点可以通过全减法器克服。全减法器是一个组合电路,具有三个输入 A、B、C 和两个输出 D 和 C'。 A 是"被减数",B 是"减数",C 是前一阶段产生的"借位",D 是差值输出,C' 是借位输出。
真值表
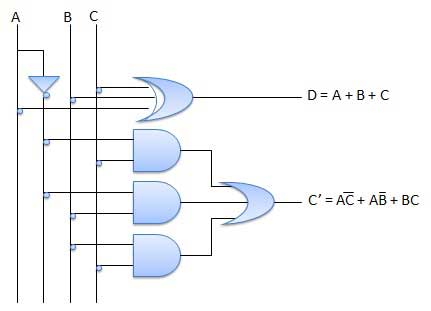
电路图
多路复用器
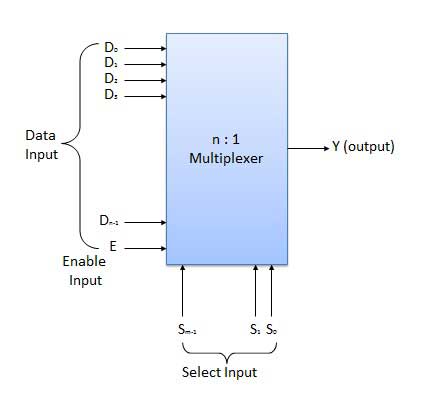
多路复用器是一种特殊类型的组合电路。有 n 个数据输入、一个输出和 m 个选择输入,其中 2m = n。它是一个数字电路,可从 n 个数据输入中选择一个并将其路由到输出。 n 个输入中的一个的选择由所选输入完成。根据所选输入上应用的数字代码,从 n 个数据源中选择一个并传输到单个输出 Y。E 称为选通或启用输入,可用于级联。它通常是一个低电平有效终端,这意味着当它处于低电平时,它将执行所需的操作。
框图
多路复用器有多种变体
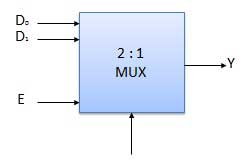
- 2 : 1 多路复用器
- 4 : 1 多路复用器
- 16 : 1 多路复用器
- 32 : 1 多路复用器
框图
真值表
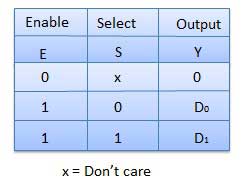
多路分解器
多路分解器执行多路复用器的逆操作,即它接收一个输入并将其分配到多个输出上。它只有一个输入、n 个输出和 m 个选择输入。每次选择线只选择一条输出线,输入将传输到所选输出线。解复用器相当于如图所示的单极多路开关。
解复用器有多种变化。
- 1 : 2 解复用器
- 1 : 4 解复用器
- 1 : 16 解复用器
- 1 : 32 解复用器
框图
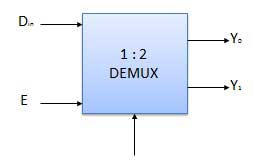
真值表
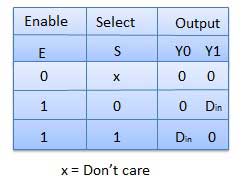
解码器
解码器是一种组合电路。它有 n 个输入和最多 m = 2n 个输出。解码器与没有任何数据输入的解复用器相同。它执行的操作与编码器的操作完全相反。
框图
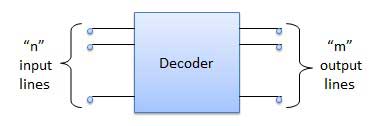
解码器示例如下。
- 代码转换器
- BCD 到七段解码器
- 数码管解码器
- 继电器执行器
2 到 4 线解码器
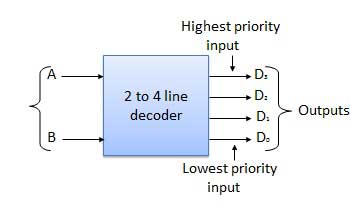
图中显示了 2 到 4 线解码器的框图。A 和 B 是两个输入,其中 D 到 D 是四个输出。真值表解释了解码器的操作。它表明,仅对于特定的输入组合,每个输出才为 1。
框图
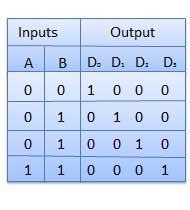
真值表
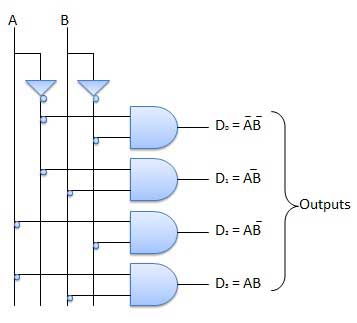
逻辑电路
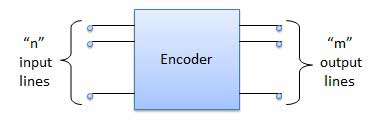
编码器
编码器是一种组合电路,用于执行解码器的逆操作。编码器有 n 条输入线和 m 条输出线。编码器产生与数字输入数相对应的 m 位二进制代码。编码器接受 n 个输入数字字并将其转换为 m 位另一个数字字。
框图
编码器示例如下。
- 优先级编码器
- 十进制到 BCD 编码器
- 八进制到二进制编码器
- 十六进制到二进制编码器
优先级编码器
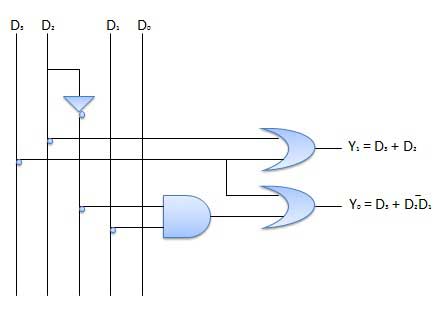
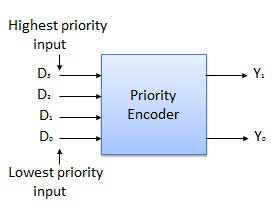
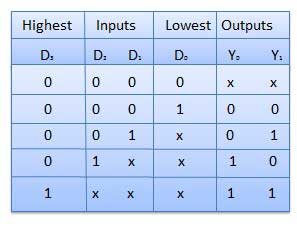
这是一种特殊类型的编码器。输入线路具有优先级。如果两条或多条输入线路同时为 1,则将考虑优先级最高的输入线路。有四个输入 D0、D1、D2、D3 和两个输出 Y0、Y1。在四个输入中,D3 具有最高优先级,而 D0 具有最低优先级。这意味着如果 D3 = 1,则 Y1 Y1 = 11,而其他输入则不考虑。类似地,如果 D3 = 0 且 D2 = 1,则 Y1 Y0 = 10,与其他输入无关。
框图
真值表
逻辑电路