Transformer 模型中的位置编码
借助输入嵌入,Transformer 可以获得离散标记(如单词、子单词或字符)的向量表示。但是,这些向量表示不提供有关这些标记在序列中的位置的信息。这就是在 Transformer 的架构中紧接着输入嵌入子层之后使用名为"位置编码"的关键组件的原因。
位置编码通过为输入序列中的每个标记提供有关其位置的信息,使模型能够理解序列顺序。在本章中,我们将了解位置编码是什么、为什么需要它、它的工作原理及其在 Python 编程语言中的实现。
什么是位置编码?
位置编码是 Transformer 中使用的一种机制,用于提供有关输入序列中标记顺序的信息。在Transformer架构中,位置编码组件被添加到输入嵌入子层之后。
请看下图;它是原始Transformer架构的一部分,表示位置编码组件的结构−
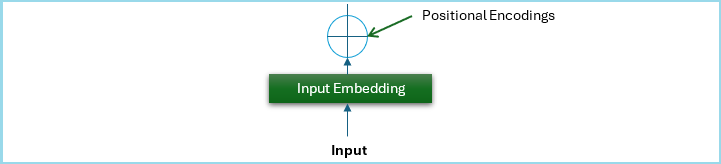
为什么Transformer模型需要位置编码?
尽管Transformer具有强大的自注意力机制,但它缺乏固有的秩序感。与按特定顺序处理序列的循环神经网络(RNN)和长短期记忆(LSTM)不同,Transformer的并行处理不提供有关输入序列中标记位置的信息。因此,模型无法理解上下文,特别是在单词顺序很重要的任务中。
为了克服这一限制,引入了位置编码,为输入序列中的每个标记提供有关其位置的信息。然后将这些编码添加到输入嵌入中,以确保 Transformer 处理标记及其位置上下文。
位置编码如何工作?
我们在上一章中讨论过,Transformer 期望位置编码函数输出的每个向量表示都有一个固定大小的维空间(可能是 dmodel = 512 或任何其他常数值)。
作为一个例子,让我们看看下面给出的句子 −
我在玩棕色球,我弟弟在玩红色球。
单词"brown"和"red"可能相似,但在这个句子中,它们相距甚远。单词"brown"位于位置 6(pos = 6),单词"red"位于位置 15(pos = 15)。
这里的问题是,我们需要找到一种方法来为输入句子中每个单词的词嵌入添加一个值,以便它具有有关其序列的信息。但是,对于每个词嵌入,我们需要找到一种方法来提供 (0, 512) 范围内的信息。
位置编码可以通过多种方式实现,但 Vashwani 等人(2017)在原始 Transformer 模型中使用了一种基于正弦函数的特定方法,为序列中的每个位置生成唯一的位置编码。
以下等式显示了给定位置 pos 和维度 i 的位置编码如何定义为 −
$$\mathrm{PE_{pos \: 2i} \: = \: sin\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)}$$
$$\mathrm{PE_{pos \: 2i+1} \: = \: cos\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)}$$
这里,dmodel 是嵌入的维度。
使用正弦函数创建位置编码
下面给出了一个使用正弦函数创建位置编码的 Python 脚本 −
def positional_encoding(max_len, d_model):
pe = np.zeros((max_len, d_model))
position = np.arange(0, max_len).reshape(-1, 1)
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
pe[:, 0::2] = np.sin(position * div_term)
pe[:, 1::2] = np.cos(position * div_term)
return pe
# 参数
max_len = len(tokens)
# 生成位置编码
pos_encodings = positional_encoding(max_len, embed_dim)
# 调整位置编码的长度以匹配输入
input_embeddings_with_pos = input_embeddings + pos_encodings[:len(tokens)]
print("位置编码:
", pos_encodings)
print("具有位置编码的输入嵌入:
", input_embeddings_with_pos)
现在,让我们看看如何将它们添加到我们在上一章中实现的输入嵌入中 −
import numpy as np
# 示例文本和标记化
text = "Transformers 彻底改变了 NLP 领域"
tokens = text.split()
# 创建词汇表
vocab = {word: idx for idx, word in enumerate(tokens)}
# 示例输入(token 索引序列)
input_indices = np.array([vocab[word] for word in tokens])
print("Vocabulary:", vocab)
print("Input Indices:", input_indices)
# 参数
vocab_size = len(vocab)
embed_dim = 512 # 嵌入的维度
# 使用随机值初始化嵌入矩阵
embedding_matrix = np.random.rand(vocab_size, embed_dim)
# 获取输入索引的嵌入
input_embeddings = embedding_matrix[input_indices]
print("Embedding Matrix:
", embedding_matrix)
print("Input Embeddings:
", input_embeddings)
def positional_encoding(max_len, d_model):
pe = np.zeros((max_len, d_model))
position = np.arange(0, max_len).reshape(-1, 1)
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
pe[:, 0::2] = np.sin(position * div_term)
pe[:, 1::2] = np.cos(position * div_term)
return pe
# 参数
max_len = len(tokens)
# 生成位置编码
pos_encodings = positional_encoding(max_len, embed_dim)
# 调整位置编码的长度以匹配输入
input_embeddings_with_pos = input_embeddings + pos_encodings[:len(tokens)]
print("Positional Encodings:
", pos_encodings)
print("Input Embeddings with Positional Encoding:
", input_embeddings_with_pos)
输出
运行上述脚本后,我们将得到以下输出 −
Vocabulary: {'Transformers': 0, 'revolutionized': 1, 'the': 2, 'field': 3, 'of': 4, 'NLP': 5}
Input Indices: [0 1 2 3 4 5]
Embedding Matrix:
[[0.71034683 0.08027048 0.89859858 ... 0.48071898 0.76495253 0.53869711]
[0.71247114 0.33418585 0.15329225 ... 0.61768814 0.32710687 0.89633072]
[0.11731439 0.97467007 0.66899319 ... 0.76157481 0.41975638 0.90980636]
[0.42299987 0.51534082 0.6459627 ... 0.58178494 0.13362482 0.13826352]
[0.2734792 0.80146145 0.75947837 ... 0.15180679 0.93250566 0.43946461]
[0.5750698 0.49106984 0.56273384 ... 0.77180581 0.18834177 0.6658962 ]]
Input Embeddings:
[[0.71034683 0.08027048 0.89859858 ... 0.48071898 0.76495253 0.53869711]
[0.71247114 0.33418585 0.15329225 ... 0.61768814 0.32710687 0.89633072]
[0.11731439 0.97467007 0.66899319 ... 0.76157481 0.41975638 0.90980636]
[0.42299987 0.51534082 0.6459627 ... 0.58178494 0.13362482 0.13826352]
[0.2734792 0.80146145 0.75947837 ... 0.15180679 0.93250566 0.43946461]
[0.5750698 0.49106984 0.56273384 ... 0.77180581 0.18834177 0.6658962 ]]
Positional Encodings:
[[ 0.00000000e+00 1.00000000e+00 0.00000000e+00 ... 1.00000000e+00
0.00000000e+00 1.00000000e+00]
[ 8.41470985e-01 5.40302306e-01 8.21856190e-01 ... 9.99999994e-01
1.03663293e-04 9.99999995e-01]
[ 9.09297427e-01 -4.16146837e-01 9.36414739e-01 ... 9.99999977e-01
2.07326584e-04 9.99999979e-01]
[ 1.41120008e-01 -9.89992497e-01 2.45085415e-01 ... 9.99999948e-01
3.10989874e-04 9.99999952e-01]
[-7.56802495e-01 -6.53643621e-01 -6.57166863e-01 ... 9.99999908e-01
4.14653159e-04 9.99999914e-01]
[-9.58924275e-01 2.83662185e-01 -9.93854779e-01 ... 9.99999856e-01
5.18316441e-04 9.99999866e-01]]
Input Embeddings with Positional Encoding:
[[0.71034683 1.08027048 0.89859858 ... 1.48071898 0.76495253 1.53869711]
[1.55394213 0.87448815 0.97514844 ... 1.61768813 0.32721053 1.89633072]
[1.02661182 0.55852323 1.60540793 ... 1.76157479 0.4199637 1.90980634]
[0.56411987 -0.47465167 0.89104811 ... 1.58178489 0.13393581 1.13826347]
[-0.4833233 0.14781783 0.1023115 ... 1.15180669 0.93292031 1.43946452]
[-0.38385447 0.77473203 -0.43112094 ... 1.77180567 0.18886009 1.66589607]]
结论
在本章中,我们介绍了位置编码的基础知识、其必要性、工作原理、Python 实现以及在 Transformer 模型中的集成。位置编码是 Transformer 架构的基本组成部分,使模型能够捕获序列中标记的顺序。
理解和实现位置编码的概念对于充分利用 Transformer 模型的潜力并有效地应用它们来解决复杂的 NLP 问题非常重要。


