HTML CSS JAVASCRIPT PYTHON PYTHON2 JAVA C C++ C# SQL Excel Linux AI BOOTSTRAP PHP 教程库 参考手册 技术文章 测验 练习 HOWTO FAQ
❮ 上一节 下一节 ❯

Transformers 中的前馈神经网络

Transformer 模型已经改变了自然语言处理 (NLP) 领域以及其他基于序列的任务。正如我们在前面章节中讨论的那样，Transformer 主要依赖于多头注意力和自注意力机制，但还有另一个关键组件同样有助于该模型的成功。这个关键组件是前馈神经网络 (FFNN)。

FFNN 子层可帮助 Transformer 捕获输入数据序列中的复杂模式和关系。阅读本章以了解 FFNN 子层、它在 Transformer 中的作用以及如何使用 Python 编程语言在 Transformer 架构中实现 FFNN。

前馈神经网络 (FFNN) 子层

在 Transformer 架构中，FFNN 子层位于多头注意力子层上方。它的输入是前一层的后层归一化后的$\mathrm{d_{model} \: = \: 15}$输出。 FFNN 是 Transformer 的一个简单但功能强大的组件，它在序列的每个位置上独立运行。

在下图中，即 Transformer 架构的编码器堆栈，您可以看到 FFNN 子层的位置(使用黑色圆圈突出显示)−

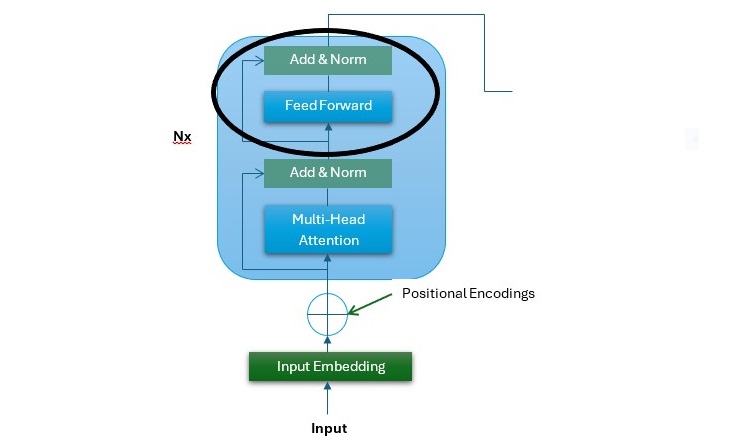
前馈神经网络子层

以下几点描述了 FFNN 子层−

  • Transformer 架构的编码器和解码器中的 FFNN 子层是完全连接的。
  • FFNN 是一个位置网络，其中每个位置都以类似的方式单独处理。
  • FFNN 包含两个线性变换并在它们之间应用激活函数。最常见的激活函数之一是 ReLU。
  • FFNN 子层的输入和输出均为 $\mathrm{d_{model} \: = \: 512}$。
  • 与输入层和输出层相比，FFNN 子层的内层较大，为 $\mathrm{d_{ff} \: = \: 2048}$。

FFNN 子层的数学表示

FFNN 子层可以用以下数学形式表示 −

第一个线性变换

$$\mathrm{X_{1} \: = \: XW_{1} \: + \: b_{1}}$$

这里，X 是 FFNN 子层的输入。$\mathrm{W_{1}}$ 是第一个线性变换的权重矩阵，$\mathrm{b_{1}}$ 是偏差向量。

ReLU 激活函数

ReLU 激活函数通过在网络中引入非线性，使网络能够学习复杂模式。

$$\mathrm{X_{2} \: = \: max(0, X_{1})}$$

第二个线性变换

$$\mathrm{Output \: = \: X_{2}W_{2} \: + \: b_{2}}$$

这里，$\mathrm{W_{2}}$是第二个线性变换的权重矩阵，$\mathrm{b_{2}}$是偏差向量。

我们结合以上步骤来总结一下FFNN子层−

$$\mathrm{Output \: = \: max(0, XW_{1} \: + \: b_{1})W_{2} \: + \: b_{2}}$$

Transformer中FFNN子层的重要性

下面给出了Transformer中FFNN子层的作用和重要性−

特征变换

FFNN子层对特征执行复杂的变换输入数据序列。借助它，模型可以从数据序列中学习详细和高级特征。

位置独立性

正如我们在上一章中讨论的那样，自注意力机制检查输入数据序列中各个位置之间的关系。但是，另一方面，FFNN子层在输入数据序列中的每个位置上独立工作。此功能增强了多头注意子层生成的表示。

前馈神经网络的Python实现

下面给出了一个分步的Python实现指南，演示了如何在Transformer架构中实现前馈神经网络子层−

步骤1:初始化FFNN的参数

在Transformer架构中，FFNN子层由两个线性变换以及它们之间的ReLU激活函数组成。在此步骤中，我们将初始化这些转换的权重矩阵和偏差向量 −

import numpy as np

class FeedForwardNN:
   def __init__(self, d_model, d_ff):
    # 第一个线性变换的权重和偏差
    self.W1 = np.random.randn(d_model, d_ff) * 0.01
    self.b1 = np.zeros((1, d_ff))
    
    # 第二个线性变换的权重和偏差
    self.W2 = np.random.randn(d_ff, d_model) * 0.01
    self.b2 = np.zeros((1, d_model))

   def forward(self, x):
    # 第一个线性变换，然后是 ReLU 激活
    x = np.dot(x, self.W1) + self.b1
    x = np.maximum(0, x) # ReLU 激活
    
    # 第二个线性变换
    x = np.dot(x, self.W2) + self.b2
    return x

步骤 2:创建示例输入数据

在此步骤中，我们将创建一些示例输入数据以通过我们的 FFNN。在 Transformer 架构中，输入通常是形状为 (batch_size、seq_len、d_model) 的张量。

# 示例输入维度
batch_size = 64 # 一批中的序列数
seq_len = 10 # 每个序列的长度
d_model = 512 # 模型的维度(输入/输出维度)

# 形状为 (batch_size、seq_len、d_model) 的随机输入张量
x = np.random.rand(batch_size、seq_len、d_model)

步骤 3:实例化和使用 FFNN

最后，我们将实例化"FeedForwardNN"类并使用上述示例输入张量执行前向传递 −

# 创建 FFNN 实例
ffnn = FeedForwardNN(d_model, d_ff=2048) # 将 d_ff 设置为内层的所需维度

# 执行前向传递
output = ffnn.forward(x)

# 打印输出形状(应为 (batch_size, seq_len, d_model))
print("输出形状:", output.shape)

完整实现示例

结合以上三个步骤即可获得完整实现示例 −

# 步骤 1 - 初始化 FFNN 的参数
import numpy as np

class FeedForwardNN:
   def __init__(self, d_model, d_ff):
    # 第一个线性变换的权重和偏差
    self.W1 = np.random.randn(d_model, d_ff) * 0.01
    self.b1 = np.zeros((1, d_ff))
    
    # 第二个线性变换的权重和偏差
    self.W2 = np.random.randn(d_ff, d_model) * 0.01
    self.b2 = np.zeros((1, d_model))

   def forward(self, x):
    # 第一个线性变换，然后是 ReLU 激活
    x = np.dot(x, self.W1) + self.b1
    x = np.maximum(0, x) # ReLU 激活
    
    # 第二个线性变换
    x = np.dot(x, self.W2) + self.b2
    return x
      
# 步骤 2 - 创建示例输入数据
# 示例输入维度
batch_size = 64 # 一批中的序列数
seq_len = 10 # 每个序列的长度
d_model = 512 # 模型的维度(输入/输出维度)

# 形状为 (batch_size, seq_len, d_model) 的随机输入张量
x = np.random.rand(batch_size, seq_len, d_model)

# 步骤 3 - 实例化和使用 FFNN
# 创建 FFNN 实例
# 将 d_ff 设置为内层的所需维度
ffnn = FeedForwardNN(d_model, d_ff=2048)

# 执行前向传递
output = ffnn.forward(x)

# 打印输出形状(应为 (batch_size, seq_len, d_model))
print("输出形状:", output.shape)

输出

运行上述脚本后，应打印输出张量的形状以验证计算 −

输出形状:(64, 10, 512)

结论

前馈神经网络 (FFNN) 子层是 Transformer 架构中必不可少的组件。它增强了模型捕获输入数据序列中复杂模式和关系的能力。

FFNN 通过独立应用位置转换来补充自注意力机制。这使得 Transformer 成为自然语言处理和其他基于序列的任务的强大模型。

在本章中，我们全面概述了 FFNN 子层、它在 Transformer 中的作用和重要性，并提供了分步指南，展示了 Transformer 中 FFNN 的 Python 实现。与多头注意力机制一样，理解和使用FFNN对于在NLP应用中充分利用Transformer模型也很重要。

❮ 上一节 下一节 ❯