李萨如图形

李萨如图形是当正弦信号同时施加到 CRO 的水平和垂直偏转板上时，屏幕上显示的图案。这些图案将根据施加到水平和垂直偏转板上的正弦信号的幅度、频率和相位差而变化。 CRO 的垂直偏转板。

下图显示了李萨如图形的一个示例。

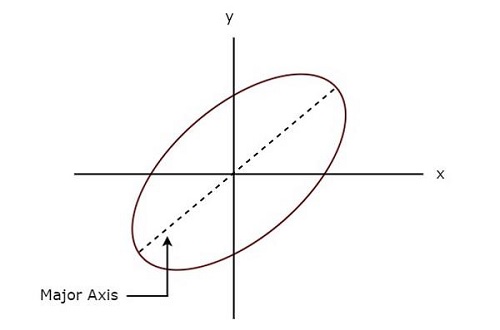
上面的李萨如图形呈椭圆形，其主轴与正 x 轴有一定的倾斜角。

使用李萨如图形进行测量

我们可以从李萨如图形中进行以下两项测量。

现在，让我们逐一讨论这两个测量。

当正弦信号施加到 CRO 的水平和垂直偏转板上时，屏幕上将显示李萨如图形。因此，将具有标准已知频率的正弦信号施加到 CRO 的水平偏转板上。同样，将频率未知的正弦信号施加到 CRO 的垂直偏转板上

假设 $f_{H}$ 和 $f_{V}$ 分别为施加到 CRO 的水平和垂直偏转板上的正弦信号的频率。 $f_{H}$ 和 $f_{V}$ 之间的关系可以数学表示如下。

$$\frac{f_{V}}{f_{H}}=\frac{n_{H}}{n_{V}}$$

从上述关系中，我们将得到施加到 CRO 垂直偏转板上的正弦信号的频率为

$f_{V}=\left ( \frac{n_{H}}{n_{V}} ight )f_{H}$(公式 1)

其中，

$n_{H}$ 是水平切线的数量

$n_{V}$ 是垂直切线的数量切线

我们可以从李萨如图形中找到 $n_{H}$ 和 $n_{V}$ 的值。因此，通过在公式 1 中代入 $n_{H}$、$n_{V}$ 和 $f_{H}$ 的值，我们将得到 $f_{V}$ 的值，即施加到 CRO 垂直偏转板上的 正弦信号的频率。

当正弦信号同时施加到 CRO 的水平和垂直偏转板上时，屏幕上会显示李萨如图形。因此，将具有相同幅度和频率的正弦信号施加到CRO的水平和垂直偏转板上。

对于一些李萨如图形，根据其形状，我们可以直接判断两个正弦信号之间的相位差。

如果李萨如图形是一条直线，其倾角为$45^{\circ}$，x轴为正，则两个正弦信号之间的相位差将为$0^{\circ}$。这意味着，这两个正弦信号之间没有相位差。
如果李萨如图形是一条直线，倾角为$135^{\circ}$，x轴为正，则两个正弦信号之间的相位差将为$180^{\circ}$。这意味着，这两个正弦信号是异相的。
如果李萨如图形是圆形，则两个正弦信号之间的相位差将为$90^{\circ}$或$270^{\circ}$。

当李萨如图形是椭圆形时，我们可以用公式计算出两个正弦信号之间的相位差。

$$\phi =\sin ^{-1}\left ( \frac{x_{1}}{x_{2}} ight )=\sin ^{-1}\left ( \frac{y_{1}}{y_{2}} ight )$$

$$\phi =180 - \sin ^{-1}\left ( \frac{x_{1}}{x_{2}} ight )=180 - \sin ^{-1}\left ( \frac{y_{1}}{y_{2}} ight )$$

其中，

$x_{1}$ 是从原点到椭圆形李萨如图形在 x 轴上的交点的距离

$x_{2}$ 是从原点到椭圆形李萨如图形的垂直切线的距离

$y_{1}$ 是从原点到椭圆形李萨如图形在 y 轴上的交点的距离相交

$y_{2}$ 是椭圆形李萨如图形的水平切线到原点的距离

本章我们学习了如何利用公式从李萨如图形中找出未知正弦信号的频率以及两个正弦信号之间的相位差。