直流电压表

直流电压表是一种测量仪器，用于测量电路中任意两点之间的直流电压。如果我们将电阻与永磁动圈 (PMMC) 检流计串联，则整个组合将一起充当直流电压表。

直流电压表中使用的串联电阻也称为串联倍增电阻或简称为倍增器。它基本上限制了流过检流计的电流量，以防止仪表电流超过满量程偏转值。直流电压表的电路图如下图所示。

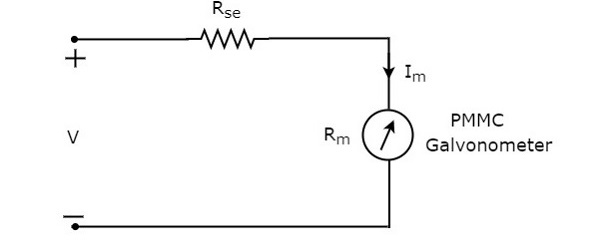
我们必须将此直流电压表放在电路中要测量直流电压的两个点之间。

在上述电路的环路周围应用KVL。

$V-I_{m}R_{se}-I_{m}R_{m}=0$ (公式 1)

$$\Rightarrow V-I_{m}R_{m}=I_{m}R_{se}$$

$$\Rightarrow R_{se}=\frac{V-I_{m}R_{m}}{I_{m}}$$

$\Rightarrow R_{se}=\frac{V}{I_{m}}-R_{m}$ (公式 2)

其中，

$R_{se}$ 为串联乘法器电阻

$V$ 为待测量的满量程直流电压

$I_{m}$ 为满量程偏转电流

$R_{m}$ 为检流计内阻

待测量的满量程直流电压 $V$ 与检流计两端的直流压降 $V_{m}$ 之比称为 乘法因子，m。从数学上讲，它可以表示为

$m=\frac{V}{V_{m}}$ （公式 3）

从公式 1，我们将得到要测量的全范围直流电压的以下公式，$V$。

$V=I_{m}R_{se}+I_{m}R_{m}$ （公式 4）

检流计上的直流电压降，$V_{m}$是满量程偏转电流，$I_{m}$和检流计内阻，$R_{m}$的乘积。从数学上来说，它可以写成

$V_{m}=I_{m}R_{m}$ （公式 5）

将公式 4 和公式 5 代入公式 3 中。

$$m=\frac{I_{m}R_{se}+I_{m}R_{m}}{I_{m}R_{m}}$$

$\Rightarrow m=\frac{R_{se}}{R_{m}}+1$

$\Rightarrow m-1=\frac{R_{se}}{R_{m}}$

$R_{se}=R_{m}\left (m-1 ight )$(公式 6)

我们可以根据现有数据，使用公式 2 或公式 6 找到串联乘法器电阻的值。

多量程直流电压表

在上一节中，我们讨论了直流电压表，它是通过将乘法电阻与 PMMC 检流计串联而获得的。此直流电压表可用于测量特定范围的直流电压。

如果我们想使用直流电压表测量多量程的直流电压，那么我们必须使用多个并联乘法电阻而不是单个乘法电阻，并且整个电阻组合与 PMMC 检流计串联。多量程直流电压表的电路图如下图所示。

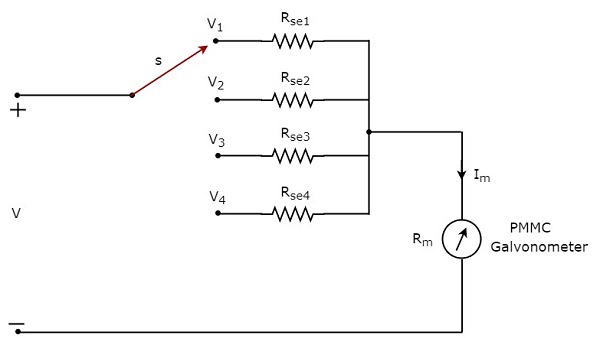
我们必须将此多量程直流电压表放置在电路的两个点上，需要测量所需范围的直流电压。我们可以通过将开关 s 连接到相应的乘法电阻来选择所需的电压范围。

当我们将要测量的全量程直流电压分别视为 $V_{1} 、V_{2}、V_{3}$ 和 $V_{4}$ 时，设 $m_{1}、m_{2}、m_{2} $ 和 $m_{4}$ 为直流电压表的乘数。以下是与每个乘数相对应的公式。

$$m_{1}=\frac{V_{1}}{V_{m}}$$

$$m_{2}=\frac{V_{2}}{V_{m}}$$

$$m_{3}=\frac{V_{3}}{V_{m}}$$

$$m_{4}=\frac{V_{4}}{V_{m}}$$

在上述电路中，有四个串联乘法电阻，$R_{se1}、R_{se2}、R_{se3}$ 和 $R_{se4}$。以下是这四个电阻对应的公式。

$$R_{se1}=R_{m}\left (m_{1}-1 ight )$$

$$R_{se2}=R_{m}\left (m_{2}-1 ight )$$

$$R_{se3}=R_{m}\left (m_{3}-1 ight )$$

$$R_{se4}=R_{m}\left (m_{4}-1 ight )$$

因此，我们可以通过上述公式找到每个串联乘法电阻的阻值。