多边形填充算法
多边形是顶点的有序列表,如下图所示。要用特定颜色填充多边形,您需要确定落在多边形边界上的像素和落在多边形内的像素。在本章中,我们将了解如何使用不同的技术填充多边形。

扫描线算法
此算法通过将扫描线与多边形边缘相交来工作,并在相交对之间填充多边形。以下步骤描述了此算法的工作原理。
步骤 1 −从给定的多边形中找出 Ymin 和 Ymax。

步骤 2 − 扫描线与多边形从 Ymin 到 Ymax 的每个边相交。命名多边形的每个交点。根据上图所示,它们被命名为 p0、p1、p2、p3。
步骤 3 − 按 X 坐标的递增顺序对交点进行排序,即 (p0, p1)、(p1, p2) 和 (p2, p3)。
步骤 4 − 填充所有位于多边形内的坐标对,并忽略交替的坐标对。
洪水填充算法
有时我们会遇到一个对象,我们想用不同的颜色填充该区域及其边界。我们可以用指定的内部颜色绘制此类对象,而不是像边界填充算法那样搜索特定的边界颜色。
它不依赖于对象的边界,而是依赖于填充颜色。换句话说,它用填充颜色替换对象的内部颜色。当不再存在原始内部颜色的像素时,算法就完成了。
再次,该算法依赖于四连接或八连接方法来填充像素。但它不是寻找边界颜色,而是寻找属于内部的所有相邻像素。
边界填充算法
边界填充算法的工作原理正如其名称所示。该算法选取对象内部的一个点并开始填充,直到它碰到对象的边界。边界的颜色和我们填充的颜色应该不同,以使该算法起作用。
在该算法中,我们假设整个对象的边界颜色相同。边界填充算法可以通过 4 连通像素或 8 连通像素实现。
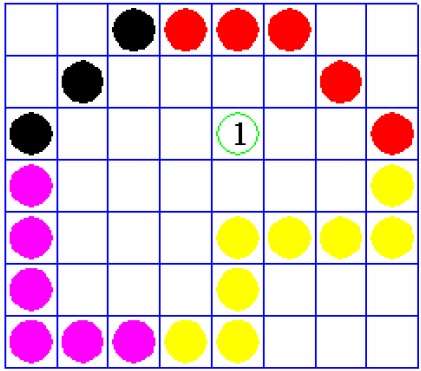
4 连通多边形
在该技术中,使用 4 连通像素,如图所示。我们将像素放在当前像素的上方、下方、右侧和左侧,这个过程将继续,直到我们找到具有不同颜色的边界。
算法
步骤 1 −初始化种子点(seedx, seedy)、fcolor、dcol的值。
步骤2 − 定义多边形的边界值。
步骤3 − 检查当前种子点是否为默认颜色,重复步骤4、5,直到到达边界像素。
If getpixel(x, y) = dcol then repeat step 4 and 5
步骤4 − 用种子点的填充颜色更改默认颜色。
setPixel(seedx, seedy, fcol)
步骤5 − 用四个邻域点递归执行该过程。
FloodFill (seedx – 1, seedy, fcol, dcol) FloodFill (seedx + 1, seedy, fcol, dcol) FloodFill (seedx, seedy - 1, fcol, dcol) FloodFill (seedx – 1, seedy + 1, fcol, dcol)
步骤 6 − 退出
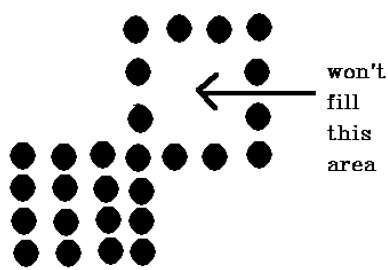
此技术存在问题。考虑如下所示的情况,我们尝试填充整个区域。此处,图像仅部分填充。在这种情况下,无法使用 4 连通像素技术。
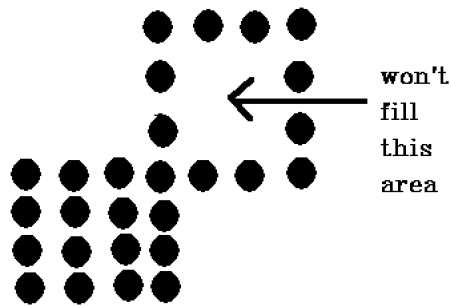
8 连通多边形
此技术中使用 8 连通像素,如图所示。我们将像素放在当前像素的上方、下方、右侧和左侧,就像我们在 4 连通技术中所做的那样。
除此之外,我们还将像素放在对角线上,以便覆盖当前像素的整个区域。这个过程会一直持续,直到我们找到一个不同颜色的边界。
算法
步骤 1 − 初始化种子点 (seedx, seedy)、fcolor 和 dcol 的值。
步骤 2 − 定义多边形的边界值。
步骤 3 − 检查当前种子点是否为默认颜色,然后重复步骤 4 和 5,直到到达边界像素
如果 getpixel(x,y) = dcol,则重复步骤 4 和 5
步骤 4 −使用种子点处的填充颜色更改默认颜色。
setPixel(seedx, seedy, fcol)
步骤 5 − Recursively follow the procedure with four neighbourhood points
FloodFill (seedx – 1, seedy, fcol, dcol) FloodFill (seedx + 1, seedy, fcol, dcol) FloodFill (seedx, seedy - 1, fcol, dcol) FloodFill (seedx, seedy + 1, fcol, dcol) FloodFill (seedx – 1, seedy + 1, fcol, dcol) FloodFill (seedx + 1, seedy + 1, fcol, dcol) FloodFill (seedx + 1, seedy - 1, fcol, dcol) FloodFill (seedx – 1, seedy - 1, fcol, dcol)
步骤 6 − 退出
4 连通像素技术无法填充下图标记的区域,而 8 连通技术则不会出现这种情况。
内外测试
此方法也称为计数法。在填充对象时,我们经常需要确定特定点是在对象内部还是外部。有两种方法可以确定特定点是位于对象内部还是外部。
- 奇偶规则
- 非零绕数规则
奇偶规则
在此技术中,我们将计算从任意点 (x,y) 到无穷远的沿线的边交叉数。如果相互作用数为奇数,则点 (x,y) 为内部点;如果相互作用数为偶数,则点 (x,y) 为外部点。以下示例描述了此概念。
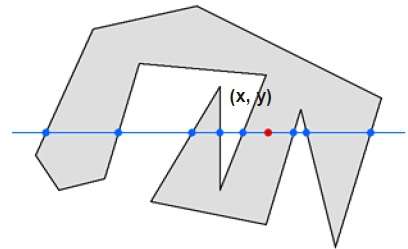
从上图可以看出,从点 (x,y) 开始,左侧的交互点数为 5,右侧的交互点数为 3。从两端开始,交互点数为奇数,因此该点被视为在对象内。
非零缠绕数规则
此方法也用于简单多边形,以测试给定点是否在内部。借助大头针和橡皮筋可以简单理解。将大头针固定在多边形的一条边上,将橡皮筋绑在里面,然后沿着多边形的边缘拉伸橡皮筋。
当橡皮筋覆盖多边形的所有边缘时,检查固定在要测试的点上的大头针。如果我们在该点处发现至少一条风,则认为该点位于多边形内,否则我们可以说该点不在多边形内。
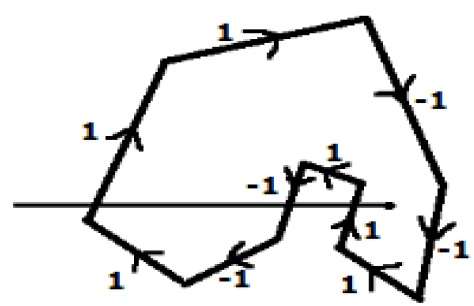
另一种替代方法是,给出多边形所有边的方向。从要测试的点向 X 方向最左边绘制一条扫描线。
将向上方向的所有边赋值为 1,将其他所有方向值赋值为 -1。
检查扫描线经过的边方向值并将它们相加。
如果此方向值的总和不为零,则要测试的这个点是内部点,否则是外部点。
在上图中,我们将扫描线经过的方向值相加,则总和为 1 – 1 + 1 = 1;不为零。因此该点被称为内部点。


