3D 计算机图形

在 2D 系统中，我们仅使用两个坐标 X 和 Y，但在 3D 中，添加了一个额外的坐标 Z。3D 图形技术及其应用是娱乐、游戏和计算机辅助设计行业的基础。它是科学可视化领域的持续研究领域。

此外，3D 图形组件现在几乎是每台个人计算机的一部分，尽管传统上用于游戏等图形密集型软件，但它们越来越多地被其他应用程序使用。

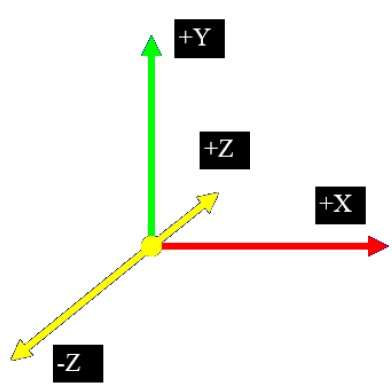
平行投影

平行投影丢弃 z 坐标，并且从对象上的每个顶点延伸平行线，直到它们与视图平面相交。在平行投影中，我们指定投影方向而不是投影中心。

在平行投影中，投影中心到投影平面的距离是无限的。在这种类型的投影中，我们通过线段连接投影顶点，这些线段对应于原始对象上的连接。

平行投影不太真实，但它们适合精确测量。在这种类型的投影中，平行线保持平行，角度不保留。以下层次结构显示了各种类型的平行投影。

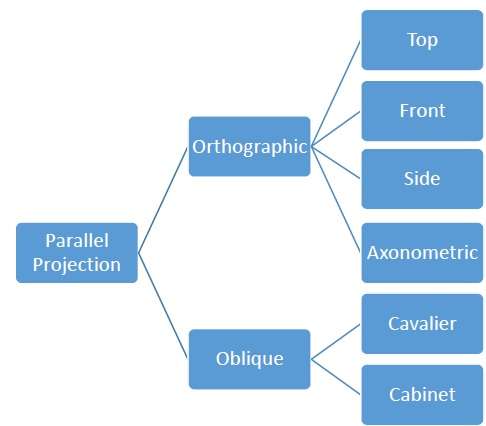
正交投影

在正交投影中，投影方向垂直于平面投影。正交投影有三种类型 −

• 正面投影
• 顶部投影
• 侧面投影

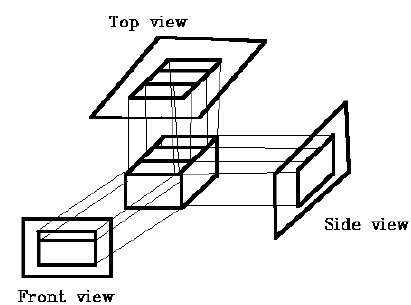
斜投影

在斜投影中，投影方向不垂直于平面投影。在斜投影中，我们可以比正交投影更好地观察物体。

斜投影有两种类型：− Cavalier 和 Cabinet。Cavalier 投影与投影平面成 45° 角。在 Cavalier 投影中，垂直于视平面的线的投影长度与线本身的长度相同。在 Cavalier 投影中，所有三个主要方向的缩短因子相等。

Cabinet 投影与投影平面成 63.4° 角。在 Cabinet 投影中，垂直于视平面的线的投影长度为其实际长度的 ½。下图显示了这两种投影 −

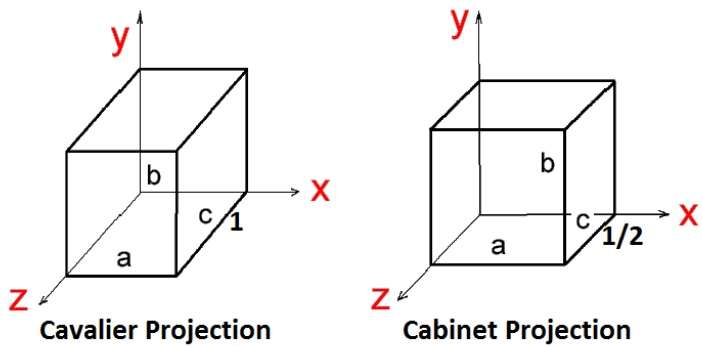
等距投影

显示物体多个侧面的正交投影称为轴测正交投影。最常见的轴测投影是等距投影，其中投影平面与模型坐标系中的每个坐标轴以相等的距离相交。在此投影中，线的平行度得以保留，但角度不得以保留。下图显示了等距投影 −

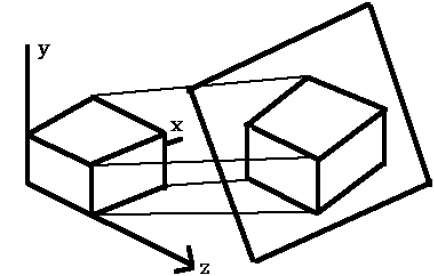
透视投影

在透视投影中，从投影中心到投影平面的距离是有限的，物体的大小与距离成反比，看起来更真实。

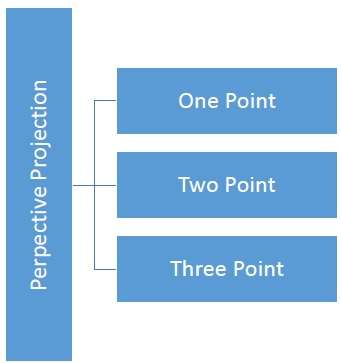
距离和角度不保留，平行线不保持平行。相反，它们都汇聚在一个称为投影中心或投影参考点的点上。透视投影有 3 种类型，如下表所示。

• 一点透视投影绘制起来很简单。

• 两点透视投影能更好地表现深度。

• 三点透视投影最难绘制。

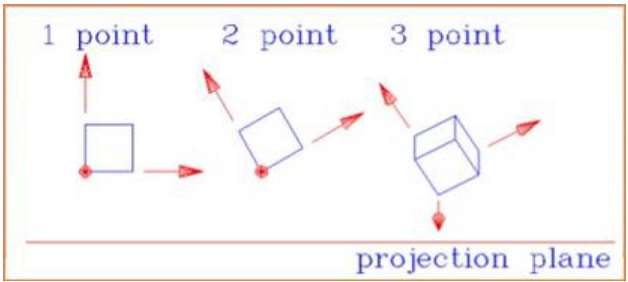
下图显示了所有三种类型的透视投影 −

平移

在 3D 平移中，我们将 Z 坐标与X 和 Y 坐标。3D 中的平移过程类似于 2D 平移。平移将对象移动到屏幕上的不同位置。

下图显示了平移 − 的效果

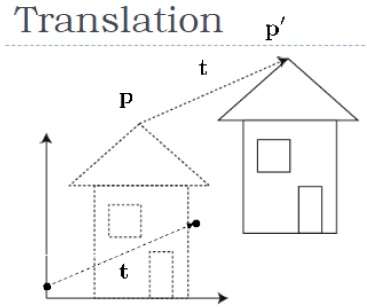
通过将平移坐标 $(t_{x,} t_{y,} t_{z})$ 添加到原始坐标 (X, Y, Z) 以获得新坐标 (X', Y', Z')，可以在 3D 中平移一个点。

$T = \begin{bmatrix} 1& 0& 0& 0\ 0& 1& 0& 0\ 0& 0& 1& 0\ t_{x}& t_{y}& t_{z}& 1\ \end{bmatrix}$

P’ = P∙T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\ 0& 1& 0& 0\ 0& 0& 1& 0\ t_{x}& t_{y}& t_{z}& 1\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$