---

2D 变换

变换是指通过应用规则将一些图形变成其他图形。我们可以进行各种类型的变换，例如平移、放大或缩小、旋转、剪切等。当变换发生在 2D 平面上时，它被称为 2D 变换。

变换在计算机图形学中起着重要作用，可以在屏幕上重新定位图形并更改其大小或方向。

同质坐标

要执行一系列变换，例如平移、旋转和缩放，我们需要遵循顺序过程 −

• 平移坐标，
• 旋转平移后的坐标，然后
• 缩放旋转后的坐标以完成复合变换。

为了缩短这个过程，我们必须使用 3×3 变换矩阵而不是 2×2 变换矩阵。要将 2×2 矩阵转换为 3×3 矩阵，我们必须添加一个额外的虚拟坐标 W。

这样，我们可以用 3 个数字而不是 2 个数字来表示该点，这称为齐次坐标系统。在这个系统中，我们可以用矩阵乘法表示所有变换方程。任何笛卡尔点 P(X, Y) 都可以通过 P' (X_h, Y_h, h) 转换为齐次坐标。

平移

平移将对象移动到屏幕上的不同位置。您可以通过将平移坐标 (t_x, t_y) 添加到原始坐标 (X, Y) 来获得新坐标 (X', Y')，从而平移 2D 中的点。

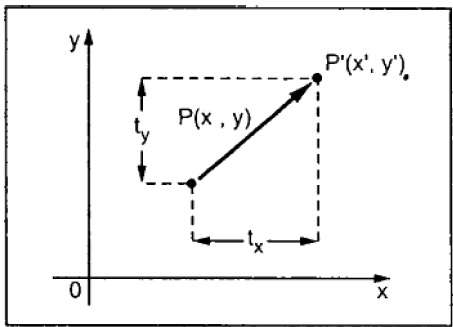
从上图，您可以写出 −

X' = X + t_x

Y' = Y + t_y

对 (t_x, t_y) 称为平移向量或移位向量。上述方程也可以用列向量表示。

$P = \frac{[X]}{[Y]}$ p' = $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$

我们可以将其写成 −

P’ = P + T

旋转

在旋转中，我们将对象从其原点旋转特定角度 θ (theta)。从下图中，我们可以看到点 P(X, Y) 位于与水平 X 坐标成角度 φ 的位置，与原点的距离为 r。

假设您想以角度 θ 旋转它。将其旋转到新位置后，您将得到一个新点 P' (X', Y')。

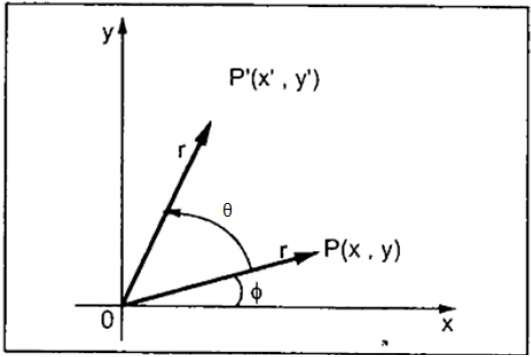
使用标准三角函数，点 P(X, Y) 的原始坐标可以表示为 −

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

同样，我们可以将点 P' (X', Y') 表示为 −

${x}'= r \: cos \: \left ( \phi \: + \: heta ight ) = r\: cos \: \phi \: cos \: heta \: − \: r \: sin \: \phi \: sin \: heta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: heta ight ) = r\: cos \: \phi \: sin \: heta \: + \: r \: sin \: \phi \: cos \: heta ....... (4)$

代入公式（1）& （2）在（3）中(4) 分别得到

${x}'= x \: cos \: heta − \: y \: sin \: heta $

${y}'= ​​x \: sin \: heta + \: y \: cos \: heta $

以矩阵形式表示上述方程，

$$[X' Y'] = [X Y] \begin{bmatrix} cos heta & sin heta \ −sin heta & cos heta \end{bmatrix}OR $$

P’ = P . R

其中 R 是旋转矩阵

$$R = \begin{bmatrix} cos heta & sin heta \ −sin heta & cos heta \end{bmatrix}$$

旋转角度可以为正也可以为负。

对于正旋转角度，我们可以使用上面的旋转矩阵。但是，对于负角度旋转，矩阵将如下所示发生变化 −

$$R = \begin{bmatrix} cos(− heta) & sin(− heta) \ -sin(− heta) & cos(− heta) \end{bmatrix}$$

$$=\begin{bmatrix} cos heta & −sin heta \ sin heta & cos heta \end{bmatrix} \left (\because cos(− heta ) = cos heta \; and\; sin(− heta ) = −sin heta ight )$$

缩放

要更改对象的大小，请使用缩放变换。在缩放过程中，您可以扩展或压缩对象的尺寸。可以通过将对象的原始坐标乘以缩放因子来实现缩放，以获得所需的结果。

假设原始坐标为 (X, Y)，缩放因子为 (S_X, S_Y)，生成的坐标为 (X', Y')。这可以用数学表示如下 −

X' = X . S_X 和 Y' = Y . S_Y

缩放因子 S_X、S_Y 分别在 X 和 Y 方向上缩放对象。上述方程也可以用矩阵形式表示如下 −

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\ 0 & S_{y} \end{bmatrix}$$

OR

P’ = P . S

其中 S 为缩放矩阵。缩放过程如下图所示。

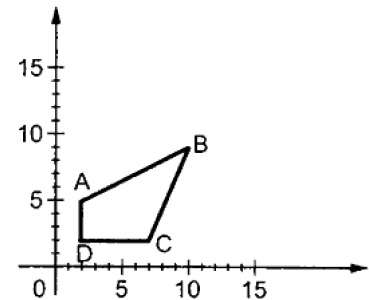
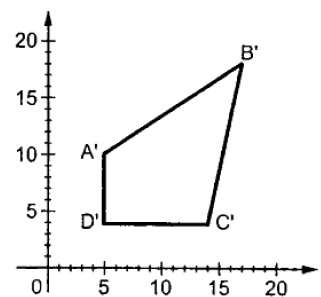
如果我们为缩放因子 S 提供小于 1 的值，则可以减小对象的尺寸。如果我们提供大于 1 的值，则可以增加对象的尺寸。

反射

反射是原始对象的镜像。换句话说，我们可以说它是一个 180° 的旋转操作。在反射变换中，物体的大小不会改变。

下图分别显示了相对于 X 轴和 Y 轴以及原点的反射。

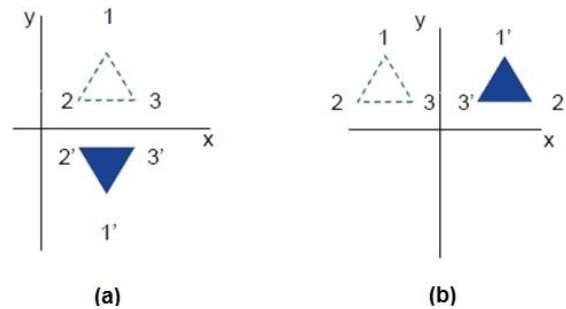
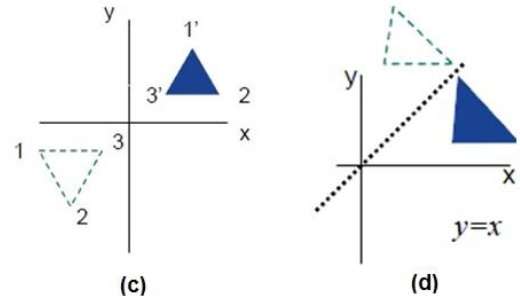
剪切

使物体形状倾斜的变换称为剪切变换。有两种剪切变换：X 剪切 和 Y 剪切。一种移动 X 坐标值，另一种移动 Y 坐标值。但是，在这两种情况下，只有一个坐标会改变其坐标，而另一个坐标会保留其值。剪切也称为倾斜。

X 剪切

X 剪切保留 Y 坐标，并对 X 坐标进行更改，这会导致垂直线向右或向左倾斜，如下图所示。

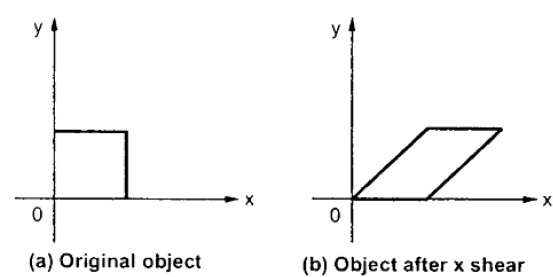
X 剪切的变换矩阵可以表示为 −

$$X_{sh} = \begin{bmatrix} 1& shx& 0\ 0& 1& 0\ 0& 0& 1 \end{bmatrix}$$

Y' = Y + Sh_y . X

X’ = X

Y 剪切

Y 剪切保留 X 坐标并改变 Y 坐标，这会导致水平线变成向上或向下倾斜的线，如下图所示。

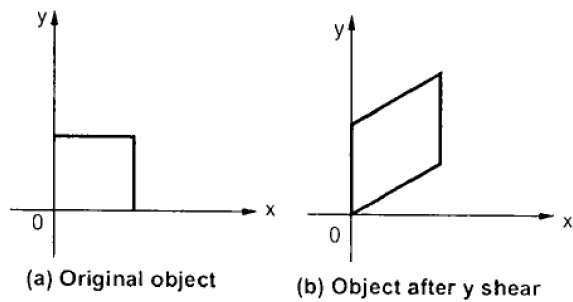
Y 剪切可以用矩阵表示为 −

$$Y_{sh} \begin{bmatrix} 1& 0& 0\ shy& 1& 0\ 0& 0& 1 \end{bmatrix}$$

X’ = X + Sh_x . Y

Y’ = Y

复合变换

如果平面 T1 的变换后跟第二个平面变换 T2，则结果本身可以用单个变换 T 表示，该变换是按顺序对 T1 和 T2 进行组合。这写为 T = T1∙T2。

复合变换可以通过将变换矩阵连接起来以获得组合变换矩阵来实现。

组合矩阵 −

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

其中 [Ti] 是下列任意组合

• 平移
• 缩放
• 剪切
• 旋转
• 反射

变换顺序的变化会导致不同的结果，因为一般来说矩阵乘法不是累积的，即 [A] . [B] ≠ [B] . [A] 和乘法顺序。组合变换的基本目的是通过将单个组合变换应用于一个点来提高效率，而不是一个接一个地应用一系列变换。

例如，要绕任意点 (X_p, Y_p) 旋转一个对象，我们必须执行三个步骤 −

• 将点 (X_p, Y_p) 平移到原点。
• 绕原点旋转。
• 最后，将旋转中心平移回其所属位置。

---