计算机图形分形

法国/美国数学家 Benoit Mandelbrot 博士发现了分形。分形一词源于拉丁语 fractus，意为破碎。

什么是分形？

分形是计算机根据单一公式生成的非常复杂的图像。它们是使用迭代创建的。这意味着一个公式会一遍又一遍地重复，值略有不同，同时考虑到上一次迭代的结果。

分形用于许多领域，例如 −

• 天文学 − 用于分析星系、土星环等。

• 生物/化学 − 用于描绘细菌培养、化学反应、人体解剖学、分子、植物等。

• 其他 − 用于描绘云、海岸线和边界线、数据压缩、扩散、经济、分形艺术、分形音乐、风景、特效等。

分形的生成

分形可以通过反复重复相同的形状来生成，如下图所示。图 (a) 显示了等边三角形。在图 (b) 中，我们可以看到三角形被重复以形成星形。在图 (c) 中，我们可以看到图 (b) 中的星形被重复多次以形成新形状。

我们可以进行无限次迭代来创建所需的形状。在编程术语中，递归用于创建此类形状。

几何分形

几何分形处理自然界中具有非整数或分形维数的形状。为了几何构造确定性（非随机）自相似分形，我们从给定的几何形状开始，称为起始器。然后将启动器的子部分替换为称为生成器的模式。

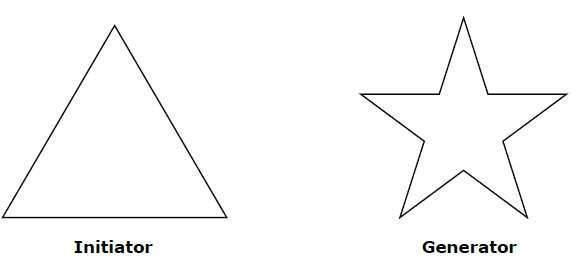
例如，如果我们使用上图所示的启动器和生成器，我们可以通过重复它来构造良好的模式。启动器中的每个直线段在每个步骤中都被四个等长的线段替换。缩放因子为 1/3，因此分形维数为 D = ln 4/ln 3 ≈ 1.2619。

此外，启动器中每个线段的长度在每个步骤中增加 4/3 倍，因此随着更多细节添加到曲线中，分形曲线的长度趋于无穷大，如下图所示 −