直线生成算法

直线连接两点，是图形的基本元素，要画直线，需要两个点，在这两个点之间画直线。在以下三个算法中，我们将直线的一点称为$X_{0}, Y_{0}$，将直线的第二个点称为$X_{1}, Y_{1}$。

DDA 算法

数字差分分析仪 (DDA) 算法是一种简单的直线生成算法，这里将逐步解释。

步骤 1 − 获取两个端点 $(X_{0}, Y_{0})$ 和 $(X_{1}, Y_{1})$ 的输入。

步骤 2 −计算两个端点之间的差值。

dx = X1 - X0
dy = Y1 - Y0

步骤 3 − 根据步骤 2 中计算出的差值，您需要确定放置像素的步数。如果 dx > dy，则您需要在 x 坐标上采取更多步骤；否则在 y 坐标上。

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

步骤4 − 计算x坐标和y坐标的增量。

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

步骤5 − 成功增加x和y坐标后，放置像素，完成线条的绘制。

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham 的线生成

Bresenham 算法是另一种增量扫描转换算法。该算法的一大优势是，它只使用整数计算。以单位间隔沿 x 轴移动，并在每一步中选择两个不同的 y 坐标。

例如，如下图所示，从位置 (2, 3) 开始，您需要在 (3, 3) 和 (3, 4) 之间进行选择。您希望点更接近原始线。

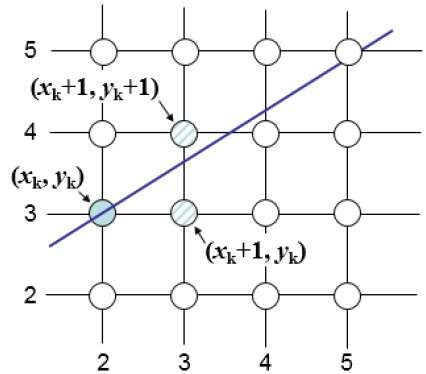
在样本位置 $X_{k}+1$，与数学线的垂直分离标记为 $d_{upper}$ 和 $d_{lower}$。

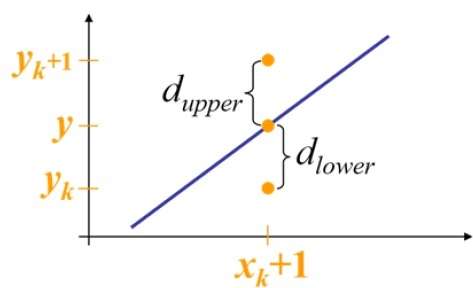
从上图可以看出，$x_{k}+1$ 处数学线上的 y 坐标为 −

Y = m($X_{k}$+1) + b

因此，$d_{upper}$ 和 $d_{lower}$ 如下所示 −

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

and

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

您可以使用这些来简单地判断哪个像素更接近数学线。这个简单的决定是基于两个像素位置之间的差异。

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

让我们用 dy/dx 代替 m，其中 dx 和 dy 是端点之间的差异。

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

因此，沿线第 k 步的决策参数 $P_{k}$ 由 −

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

决策参数 $P_{k}$ 的符号与 $d_{lower} - d_{upper}$ 的符号相同。

如果 $p_{k}$ 为负，则选择下像素，否则选择上像素像素。

请记住，坐标变化沿 x 轴以单位步骤发生，因此您可以使用整数计算完成所有操作。在步骤 k+1 时，决策参数为 −

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

从中减去 $p_{k}$ 可得到 −

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

但是，$x_{k+1}$ 与 $(xk)+1$ 相同。所以 −

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

其中，$Y_{k+1} – Y_{k}$ 为 0 或 1，具体取决于 $P_{k}$ 的符号。

第一个决策参数 $p_{0}$ 在 $(x_{0}, y_{0})$ 处求值，结果为 −

$$p_{0} = 2dy - dx$$

现在，记住以上所有要点和计算，这里是斜率 m < 1 − 的 Bresenham 算法

步骤 1 −输入线的两个端点，将左端点存储在$(x_{0}, y_{0})$中。

步骤 2 − 绘制点$(x_{0}, y_{0})$。

步骤 3 − 计算常数 dx、dy、2dy 和 (2dy – 2dx)，并获取决策参数的第一个值作为 −

$$p_{0} = 2dy - dx$$

步骤 4 − 在线上每个 $X_{k}$ 处，从 k = 0 开始，执行以下测试 −

如果 $p_{k}$ < 0，下一个要绘制的点是（x_{k}+1，y_{k}）并且

$$p_{k+1} = p_{k} + 2dy$$ Otherwise,

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

步骤 5 − 重复步骤 4 (dx – 1) 次。

对于 m > 1，确定是否需要每次增加 x 并增加 y。

求解后，决策参数 $P_{k}$ 的方程将非常相似，只是方程中的 x 和 y 互换了。

中点算法

中点算法源于 Bresenham，由 Pitteway 和 Van Aken 修改。假设您已经将点 P 放在 (x, y) 坐标处，直线的斜率为 0 ≤ k ≤ 1，如下图所示。

现在您需要决定将下一个点放在 E 还是 N。这可以通过确定最接近点 N 或 E 的交点 Q 来选择。如果交点 Q 最接近点 N，则 N 被视为下一个点；否则为 E。

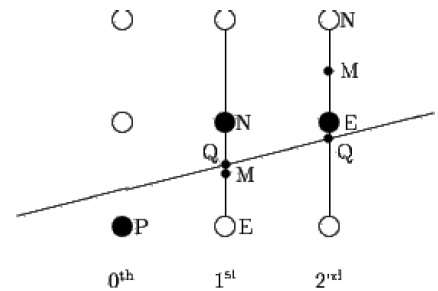
要确定这一点，首先计算中点 M(x+1, y + ½)。如果直线与连接 E 和 N 的垂直线的交点 Q 在 M 下方，则将 E 作为下一个点；否则将 N 作为下一个点。

为了检查这一点，我们需要考虑隐式方程 −

F(x,y) = mx + b - y

对于任何给定 X 处的正 m，

• 如果 y 在线上，则 F(x, y) = 0
• 如果 y 在线上方，则 F(x, y) < 0
• 如果 y 低于该线，则 F(x, y) > 0